题目内容
12.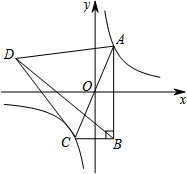 如图,已知双曲线y=$\frac{k}{x}$(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20$\sqrt{3}$,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k=( )
如图,已知双曲线y=$\frac{k}{x}$(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20$\sqrt{3}$,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 根据等边三角形的性质得出其边长,再利用勾股定理得出BC,AB的长,进而结合反比例函数的性质得出k的值.
解答 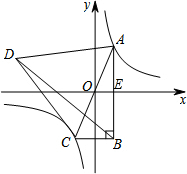 解:∵以AC为边作等边三角形ACD,且S△ACD=20$\sqrt{3}$,
解:∵以AC为边作等边三角形ACD,且S△ACD=20$\sqrt{3}$,
∴设AC的长为x,则AC边上的高为:$\frac{\sqrt{3}}{2}$x,
故$\frac{1}{2}$x×$\frac{\sqrt{3}}{2}$x=20$\sqrt{3}$,
解得:x=4$\sqrt{5}$(负数舍去),
即AC=4$\sqrt{5}$,
∵△ABD的周长比△BCD的周长多4,
由AD=DC,BD是公共边,
∴AB-BC=4,
设BC=y,则AB=4+y,
故y2+(4+y)2=(4$\sqrt{5}$)2,
解得:y1=4,y2=-8(不合题意舍去),
∴BC=4,AB=8,
由反比例函数的性质可得:AO=CO,
∵OE∥BC,
∴△AOE∽△ACB,
∴$\frac{OE}{BC}$=$\frac{AE}{AB}$=$\frac{1}{2}$,
则EO=2,AE=4,
故k=2×4=8.
故选:D.
点评 此题主要考查了反比例函数综合以及相似三角形的判定与性质以及勾股定理等知识,正确得出AC的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知方程①2x+y=0;②$\frac{1}{2}$x+y=2;③x2-x+1=0;④2x+y-3z=7是二元一次方程的是( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ① |
4.下列运算正确的为( )
| A. | (4xy2)2=8x2y4 | B. | 3x2=9x2 | C. | (-x)7÷(-x)2=-x5 | D. | (6xy2)2÷2xy=3xy3 |
2.2013年10月27日CCTV Music Radio音乐之声“让爱回家”石家庄站在石家庄某商场举办公益活动,在某一时段内,小丽统计捐款金额和捐款人数如下表所示:
则以下说法正确的是( )
| 金额/元 | 100 | 200 | 500 | 1000 |
| 人数 | 4 | 3 | 2 | 1 |
| A. | 众数是100,中位数是200 | B. | 众数是200,中位数是500 | ||
| C. | 平均数是300,方差是400 | D. | 平均数是400,方差是300 |
 如图,在△ABC中,∠ACB=90°,点O是三角形内的一点,且S△OAB=S△OBC=S△OAC,那么$\frac{O{A}^{2}+O{B}^{2}}{O{C}^{2}}$值为5.
如图,在△ABC中,∠ACB=90°,点O是三角形内的一点,且S△OAB=S△OBC=S△OAC,那么$\frac{O{A}^{2}+O{B}^{2}}{O{C}^{2}}$值为5. 如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.
如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.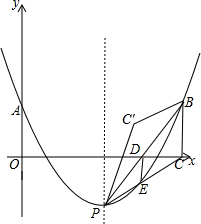 如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
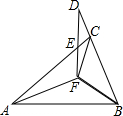 如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25,则∠AED的度数为130°.
如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25,则∠AED的度数为130°.