题目内容
16.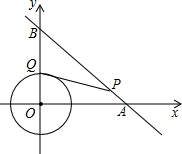 如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 8-2$\sqrt{3}$ | D. | 2$\sqrt{13}$ |
分析 由P在直线y=-x+8上,设P(m,8-m),连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,在直角三角形OPQ中,利勾股定理列出关系式,配方后利用二次函数的性质即可求出PQ的最小值.
解答 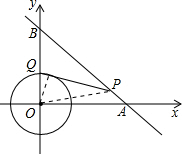 解:∵P在直线y=-x+8上,
解:∵P在直线y=-x+8上,
∴设P坐标为(m,8-m),
连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,
在Rt△OPQ中,根据勾股定理得:OP2=PQ2+OQ2,
∴PQ2=m2+(8-m)2-12=2m2-16m+52=2(m-4)2+20,
则当m=4时,切线长PQ的最小值为2$\sqrt{5}$.
故选:B.
点评 此题考查了一次函数综合题,涉及的知识有:切线的性质,勾股定理,配方法的应用,以及二次函数的性质,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
6.下列各式中,不能应用平方差公式进行计算的是( )
| A. | (a+b)(a-b) | B. | (x+2y)(x-2y) | C. | (-a-3)(-a+3) | D. | (2a-b)(-2a+b) |
1.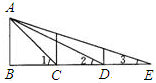 如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )
如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )
 如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )
如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )| A. | ∠1+∠2+∠3=135° | B. | △ABD∽△EBA | C. | △ACD∽△ECA | D. | 以上结论都不对 |
8.函数y=$\sqrt{2-x}$中自变量x的取值范围是( )
| A. | x>2 | B. | x≤2 | C. | x≥2 | D. | x≠2 |
6.已知a,b是方程x2+2x-5=0的两个实数根,则a2-ab+3a+b的值为( )
| A. | 2 | B. | 3 | C. | -2 | D. | 8 |
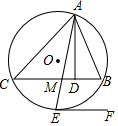 如图,AD是△ABC的高,∠BAC的平分线AM的延长线交△ABC的外接圆⊙O于点E.过点E作⊙O的切线EF.
如图,AD是△ABC的高,∠BAC的平分线AM的延长线交△ABC的外接圆⊙O于点E.过点E作⊙O的切线EF.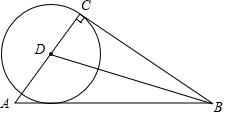 如图,Rt△ABC中,∠C=90°,BD是△ABC的平分线,交AC于点D,以点D为圆心、DC为半径作⊙D.
如图,Rt△ABC中,∠C=90°,BD是△ABC的平分线,交AC于点D,以点D为圆心、DC为半径作⊙D.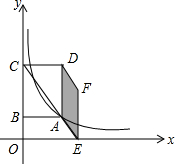 如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )
如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )