题目内容
7.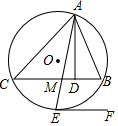 如图,AD是△ABC的高,∠BAC的平分线AM的延长线交△ABC的外接圆⊙O于点E.过点E作⊙O的切线EF.
如图,AD是△ABC的高,∠BAC的平分线AM的延长线交△ABC的外接圆⊙O于点E.过点E作⊙O的切线EF.(1)求证:EF∥BC;
(2)若AC=4cm,AB=3cm,AD=2.5cm,求⊙O的半径长.
分析 (1)连接OE,如图,利用角平分线的定义得到∠CAE=∠BAE,则$\widehat{BE}$=$\widehat{CE}$,根据垂径定理的推论得到OE⊥BC,再根据切线的性质得OE⊥EF,所以EF∥BC;
(2)作直径AH,连接CH,如图,利用圆周角定理得到∠AHC=90°,∠AEC=∠B,则可证明Rt△AHC∽Rt△ABD,然后利用相似比可计算出AH,从而得到⊙O的半径长.
解答 (1)证明:连接OE,如图,
∵AE平分∠BAC,
∴∠CAE=∠BAE,
∴$\widehat{BE}$=$\widehat{CE}$,
∴OE⊥BC,
∵EF为切线,
∴OE⊥EF,
∴EF∥BC;
(2)作直径AH,连接CH,如图,
∵AH为直径,
∴∠AHC=90°,
∵AD为高,
∴∠ADB=90°,
∵∠AEC=∠B,
∴Rt△AHC∽Rt△ABD,
∴AH:AB=AC:AD,即AH:3=4:2.5,解得AH=$\frac{24}{5}$,
∴⊙O的半径长为$\frac{12}{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理和相似三角形的判定与性质.

练习册系列答案
相关题目
12.不等式组$\left\{\begin{array}{l}{x+2>1}\\{3-x≥0}\end{array}\right.$的解是( )
| A. | x<-1 | B. | x≥3 | C. | -1<x≤3 | D. | 无解 |
19.下列方程中,属于二元一次方程的是 ( )
| A. | 2x-3y=z | B. | 5-x=$\frac{2}{y}$+1 | C. | x+y=0 | D. | 2 x2-x=5 |
16.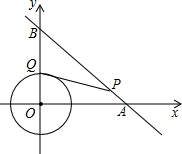 如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
 如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 8-2$\sqrt{3}$ | D. | 2$\sqrt{13}$ |
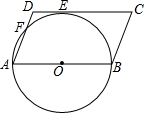 如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为π.
如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为π.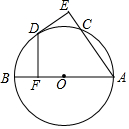 如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC的延长线于E,DF⊥AB于F.
如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC的延长线于E,DF⊥AB于F.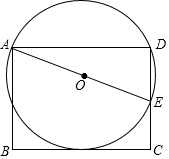 如图,点E为矩形ABCD中CD边上的一点,AB=3,AD=4,以AE为直径的⊙O恰好与BC边相切,则⊙O的半径为$\frac{13}{6}$.
如图,点E为矩形ABCD中CD边上的一点,AB=3,AD=4,以AE为直径的⊙O恰好与BC边相切,则⊙O的半径为$\frac{13}{6}$.