题目内容
16．在π，$\frac{22}{7}$，-$\sqrt{3}$，$\root{3}{343}$，3.1415，0.$\stackrel{．}{3}$，-$\frac{\sqrt{2}}{6}$，-2.10101010…，5.1717717771…中，有理数的个数有（ ）| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
分析 利用有理数定义判断即可．
解答 解：在π，$\frac{22}{7}$，-$\sqrt{3}$，$\root{3}{343}$，3.1415，0.$\stackrel{．}{3}$，-$\frac{\sqrt{2}}{6}$，-2.10101010…，5.1717717771…中，
有理数的个数有$\frac{22}{7}$，$\root{3}{343}$，3.1415，0.$\stackrel{．}{3}$，-2.10101010…，共5个，
故选B
点评 此题考查了实数，熟练掌握有理数的定义是解本题的关键．
练习册系列答案
相关题目
7．若x＜2，化简$\sqrt{（x-2）^{2}}$+|3-x|的正确结果是（ ）
| A． | -1 | B． | 1 | C． | 2x-5 | D． | 5-2x |
4．下列计算正确的是（ ）
| A． | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B． | $\sqrt{2}×\sqrt{5}=\sqrt{10}$ | C． | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | D． | $\sqrt{8}÷\sqrt{2}=4$ |
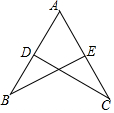如图所示，已知点D、E分别在AB、AC上，AD=AE，∠BDC=∠CEB，则BD=CE．
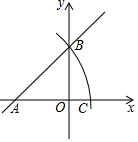如图，在平面直角坐标系中，直线y=x+b交x轴于点A，交y轴于点B，以点A为圆心，线段AB长为半径作圆弧，交x轴正半轴于点C，若AC=$\sqrt{2}$，则b的值为1．