题目内容
11.若|x-2y-1|+(2x-y-5)2=0,则xy的值为3.分析 利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可确定出原式的值.
解答 解:∵|x-2y-1|+(2x-y-5)2=0,
∴$\left\{\begin{array}{l}{x-2y=1①}\\{2x-y=5②}\end{array}\right.$,
②-①×2得:3y=3,
解得:y=1,
把y=1代入①得:x=3,
则原式=3,
故答案为:3
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
1.点(-1,a2+1)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.点A(2,y1)、B(3,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
19.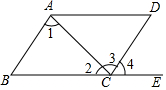 如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )
如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )
 如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )
如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )| A. | ①②④ | B. | ①② | C. | ①②③ | D. | ①②③④ |
6.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=3 | D. | $\frac{3}{\sqrt{3}}$=$\sqrt{3}$ |
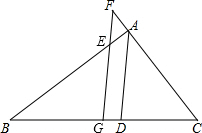 如图,AD是△ABC的角平分线,G是BC中点,FG∥AD,交AB于E,交CA的延长线于F,AC=3.8,AB=7.4,则AF=1.8.
如图,AD是△ABC的角平分线,G是BC中点,FG∥AD,交AB于E,交CA的延长线于F,AC=3.8,AB=7.4,则AF=1.8. 如图,正方形OABC的边长为4$\sqrt{2}$,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为-$\frac{1}{12}$.
如图,正方形OABC的边长为4$\sqrt{2}$,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为-$\frac{1}{12}$.