题目内容
6.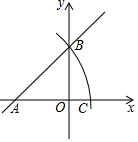 如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=$\sqrt{2}$,则b的值为1.
如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=$\sqrt{2}$,则b的值为1.
分析 根据以点A为圆心,线段AB长为半径作圆弧,可得AB=AC,进而利用待定系数法确定函数关系式即可.
解答 解:因为以点A为圆心,线段AB长为半径作圆弧,
所以AB=AC=$\sqrt{2}$,
把点A和点B坐标代入可得:$\left\{\begin{array}{l}{0=x+b}\\{y=b}\end{array}\right.$,
且$\sqrt{{x}^{2}+{y}^{2}}=\sqrt{2}$,
可得:$\sqrt{(-b)^{2}+{b}^{2}}=\sqrt{2}$,
所以b=1,
故答案为:1.
点评 此题考查待定系数法确定函数关系式问题,关键是根据以点A为圆心,线段AB长为半径作圆弧,可得AB=AC.

练习册系列答案
相关题目
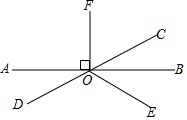 如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O,
如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O, 如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3.
如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3. 如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.
如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.