题目内容
14.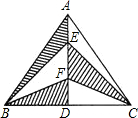 如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.
如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.
分析 根据等腰三角形性质得到AD⊥BC,推出△CEF和△BEF关于直线AD对称,得出S△BEF=S△CEF,根据图中阴影部分的面积是$\frac{1}{2}$S△ABC求出即可.
解答 解:∵AB=AC=10cm,BD=CD=6cm,AD是△ABC的中线,
∴AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
由勾股定理得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=8cm,
∵△ABC的面积=$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×(6+6)×8=48cm2,
∴图中阴影部分的面积是$\frac{1}{2}$S△ABC=24cm2.
故答案为:24.
点评 本题考查了勾股定理、轴对称的性质.通过观察可以发现是轴对称图形,且阴影部分的面积为全面积的一半,根据轴对称图形的性质求解.其中看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.

练习册系列答案
相关题目
5.点M(-4,-1)关于y轴对称的点的坐标为( )
| A. | (-4,1) | B. | (4,1) | C. | (4,-1) | D. | (-4,-1) |
 如图,在三角形ABC中,AB=AC,D为BC的中点,若∠BAD=45°,BD=3,则AD=3.
如图,在三角形ABC中,AB=AC,D为BC的中点,若∠BAD=45°,BD=3,则AD=3.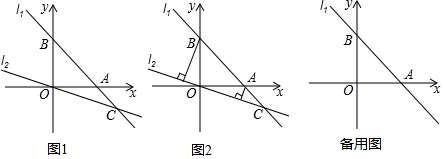
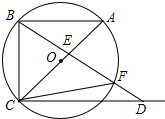 如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.
如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.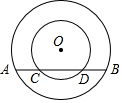 如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20.
如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20.