题目内容
5.点M(-4,-1)关于y轴对称的点的坐标为( )| A. | (-4,1) | B. | (4,1) | C. | (4,-1) | D. | (-4,-1) |
分析 根据平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点:关于y轴对称的点,纵坐标相同,横坐标互为相反数.
解答 解:∵平面直角坐标系中关于y轴对称的点的坐标特点:横坐标相反数,纵坐标不变,
可得:点M关于y轴的对称点的坐标是(4,-1).
故选:C.
点评 本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.

练习册系列答案
相关题目
10.关于x的分式方程$\frac{x-a}{x-1}$-$\frac{3}{x}$=1无解,则a的值( )
| A. | a=1 | B. | a=-2 或a=1 | C. | a=-5 | D. | a=-2或a=-5 |
17.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓线DFE所在抛物线的函数解析式为( )
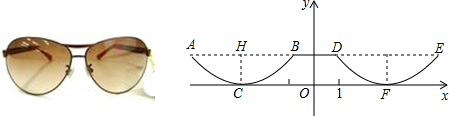

| A. | $y=\frac{1}{4}{(x+3)^2}$ | B. | $y=-\frac{1}{4}{(x+3)^2}$ | C. | $y=-\frac{1}{4}{(x-3)^2}$ | D. | $y=\frac{1}{4}{(x-3)^2}$ |
15.若双曲线y=$\frac{k}{x}$(k>0)过两点(-1,y1),(-2,y2),则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1与y2大小无法确定 |
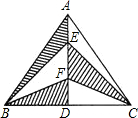 如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.
如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.