题目内容
7.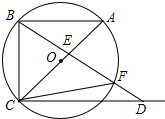 如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.
如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.(1)求线段BD的长;
(2)线段CF的长为$\frac{16}{5}$(直接填空)
分析 (1)根据直径所对的圆周角是直角可得∠ABC=90°,然后利用勾股定理列式求出AC,再根据两直线平行,同旁内角互补求出∠BCD=90°,然后利用勾股定理列式计算即可得解;
(2)连接AF,根据直径所对的圆周角是直角可得∠AFC=90°,再根据同弧所对的圆周角相等可得∠CBD=∠CAF,然后求出△ACF和△BDC相似,利用相似三角形对应边成比例列式计算即可得解.
解答 解:(1)∵AC为⊙O的直径,
∴∠ABC=90°,
在Rt△ABC中,由勾股定理得,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{(\sqrt{7})^{2}+{3}^{2}}$=4,
∵AC=CD,
∴CD=4,
∵AB∥CD,
∴∠BCD=180°-∠ABC=180°-90°=90°,
在Rt△BCD中,由勾股定理得,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;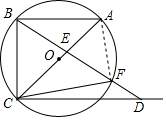
(2)如图,连接AF,
∵AC为⊙O的直径,
∴∠AFC=90°,
∴∠BCD=AFC=90°,
又∵∠CBD=∠CAF(同弧所对的圆周角相等),
∴△ACF∽△BDC,
∴$\frac{AC}{BD}$=$\frac{CF}{CD}$,
即$\frac{4}{5}$=$\frac{CF}{4}$,
解得CF=$\frac{16}{5}$.
故答案为:$\frac{16}{5}$.
点评 本题考查了相似三角形的判定与性质,圆周角定理,勾股定理,作辅助线,构造出相似三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.某地两种移动电话计费方式列表如表:
(1)一个月内,若通话时间分别为100分钟、200分钟或x分钟时,按两种计费方式各需
交费多少元?(请将未完成的答案填在表格内)
(2)当本地通话为x分钟时,请求出用全球通的话费与用神州行的话费的差.
(3)如果某个月通话时间为500分钟,用哪种计费方式更省钱?省多少元?
| 全球通 | 神州行 | |
| 月租费 | 30元/月 | 0 |
| 本地通话费 | 0.10元/分钟 | 0.30元/分钟 |
交费多少元?(请将未完成的答案填在表格内)
| 全球通(元) | 神州行(元) | |
| 100分 | 30+100×0.10=40元 | 100×0.30=30元 |
| 200分 | 30+200×0.10=50元 | 200×0.30=60元 |
| x分钟 | (30+0.1x)元 | 0.3x元 |
(3)如果某个月通话时间为500分钟,用哪种计费方式更省钱?省多少元?
17.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓线DFE所在抛物线的函数解析式为( )
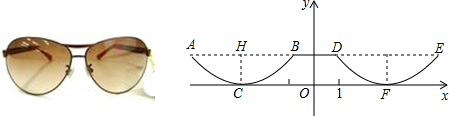

| A. | $y=\frac{1}{4}{(x+3)^2}$ | B. | $y=-\frac{1}{4}{(x+3)^2}$ | C. | $y=-\frac{1}{4}{(x-3)^2}$ | D. | $y=\frac{1}{4}{(x-3)^2}$ |
 如图:直线a∥b,∠1=42°,则∠2=138°.
如图:直线a∥b,∠1=42°,则∠2=138°.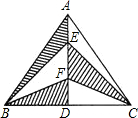 如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.
如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.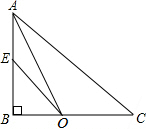 在△ABC中,∠ABC=90°,∠BAC的平分线AO交BC于O点,E为边AB上一点,且OE=OC,若AC=10,AB=6,求AE的长.
在△ABC中,∠ABC=90°,∠BAC的平分线AO交BC于O点,E为边AB上一点,且OE=OC,若AC=10,AB=6,求AE的长.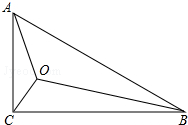 在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=$\sqrt{7}$.
在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=$\sqrt{7}$.