题目内容
4.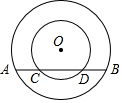 如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20.
如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20.
分析 解决此题首先要弄清楚AB在什么时候最大,什么时候最小.当AB与小圆相切时有一个公共点,此时可知AB最小;当AB经过同心圆的圆心时,弦AB最大且与小圆相交有两个公共点,此时AB最大,由此可以确定所以AB的取值范围.
解答 解:如图所示,
当AB与小圆相切时有一个公共点D,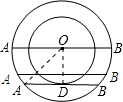
连接OA,OD,可得OD⊥AB,
∴D为AB的中点,即AD=BD,
在Rt△ADO中,OD=6,OA=10,
∴AD=8,
∴AB=2AD=16;
当AB经过同心圆的圆心时,弦AB最大且与小圆相交有两个公共点,
此时AB=20,
所以AB的取值范围是16<AB≤20.
故答案为:16<AB≤20.
点评 此题考查了直线与圆的位置关系,涉及的知识有:垂径定理,勾股定理,以及切线的性质,其中解题的关键是抓住两个关键点:1、当弦AB与小圆相切时最短;2、当AB过圆心O时最长.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.下列方程中,一定是关于x的一元二次方程的是( )
| A. | (k2+1)x2-4=0 | B. | ax2+bx+c=0 | C. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-3=0 | D. | (x+4)(x-2)=x2 |
12.某地两种移动电话计费方式列表如表:
(1)一个月内,若通话时间分别为100分钟、200分钟或x分钟时,按两种计费方式各需
交费多少元?(请将未完成的答案填在表格内)
(2)当本地通话为x分钟时,请求出用全球通的话费与用神州行的话费的差.
(3)如果某个月通话时间为500分钟,用哪种计费方式更省钱?省多少元?
| 全球通 | 神州行 | |
| 月租费 | 30元/月 | 0 |
| 本地通话费 | 0.10元/分钟 | 0.30元/分钟 |
交费多少元?(请将未完成的答案填在表格内)
| 全球通(元) | 神州行(元) | |
| 100分 | 30+100×0.10=40元 | 100×0.30=30元 |
| 200分 | 30+200×0.10=50元 | 200×0.30=60元 |
| x分钟 | (30+0.1x)元 | 0.3x元 |
(3)如果某个月通话时间为500分钟,用哪种计费方式更省钱?省多少元?
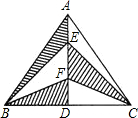 如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.
如图,在△ABC中,AB=AC=10cm,BD=CD=6cm,则图中阴影部分的面积是24cm2.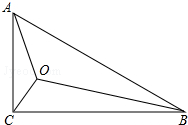 在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=$\sqrt{7}$.
在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=$\sqrt{7}$.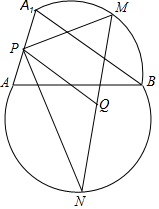 AB是圆的一条弦,它将圆分成两部分,M、N分别是两段弧的中点,以点B旋转中心将弓形AMB顺时针旋转一个角度成弓形A1MB、A1A的中点为P,MN的中点为Q.
AB是圆的一条弦,它将圆分成两部分,M、N分别是两段弧的中点,以点B旋转中心将弓形AMB顺时针旋转一个角度成弓形A1MB、A1A的中点为P,MN的中点为Q.