题目内容
 如图,在?ABCD中,O是AC与BD的交点,过点O的直线分别与AB、CD的延长线交于点E、F.当AC与EF满足什么条件时,四边形AECF是菱形?请给出证明.
如图,在?ABCD中,O是AC与BD的交点,过点O的直线分别与AB、CD的延长线交于点E、F.当AC与EF满足什么条件时,四边形AECF是菱形?请给出证明.考点:菱形的判定,全等三角形的判定与性质,平行四边形的性质
专题:
分析:先证△EBO≌△FDO,推出EO=FO,得出四边形AECF是平行四边形,再根据菱形的判定推出即可.
解答:答:当AC⊥EF时,四边形AECF是菱形,
证明:∵在□ABCD,AO=CO,BO=DO,AB∥CD,
∴∠AEO=∠CFO.
在△EBO与△FDO中
∴△EBO≌△FDO(AAS),
∴EO=FO,
又∵AO=CO,
∴四边形AECF是平行四边形.
∴AC⊥EF时,平行四边形AECF是菱形.
证明:∵在□ABCD,AO=CO,BO=DO,AB∥CD,
∴∠AEO=∠CFO.
在△EBO与△FDO中
|
∴△EBO≌△FDO(AAS),
∴EO=FO,
又∵AO=CO,
∴四边形AECF是平行四边形.
∴AC⊥EF时,平行四边形AECF是菱形.
点评:本题考查了平行线的性质,平行四边形的性质和判定,菱形的判定,全等三角形的性质和判定的应用,注意:对角线互相垂直的平行四边形是菱形.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,则AB边上的中线长为( )
| A、1 | ||
| B、2 | ||
| C、1.5 | ||
D、
|

 如图,在△ABC与△BAD中,AD与BC相交于点E,∠C=∠D,EA=EB.
如图,在△ABC与△BAD中,AD与BC相交于点E,∠C=∠D,EA=EB.
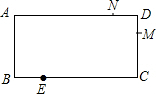 如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,当动点M回到点D时,M、N两点均停止运动.
如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,当动点M回到点D时,M、N两点均停止运动.