题目内容
如图，在△ABC与△BAD中，AD与BC相交于点E，∠C=∠D，EA=EB．求证：BC=AD．
考点：全等三角形的判定与性质
专题：证明题
分析：由已知∠C=∠D，EA=EB，以及对顶角相等，利用AAS得到三角形CAE与三角形DBE全等，利用全等三角形对应边相等得到CE=DE，等量代换即可得证．
解答：证明：在△CAE和△DBE中，
，
∴△CAE≌△DBE（AAS），
∴CE=DE，
∵EA=EB，
∴CE+EB=DE+EA，即BC=AD．
|
∴△CAE≌△DBE（AAS），
∴CE=DE，
∵EA=EB，
∴CE+EB=DE+EA，即BC=AD．
点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
相关题目
测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5m远的水底，竹竿高出水面0.5m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（ ）
| A、2.5m | B、2.25m |
| C、2m | D、3m |
如图，在?ABCD中，O是AC与BD的交点，过点O的直线分别与AB、CD的延长线交于点E、F．当AC与EF满足什么条件时，四边形AECF是菱形？请给出证明．
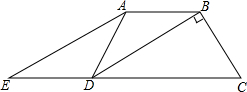如图，在四边形ABCD中，AB∥DC，DB平分∠ADC，E是CD的延长线上一点，且∠AEC=