题目内容
已知正比例函数y=mx与一次函数y=nx+b的图象交于点A(8,6),一次函数的图象与x轴交于点B,且OB=
OA.
(1)求这两个函数的解析式;
(2)若N为一次函数y=nx+b图象上的一点,且S△OBN:S△AON=1:2,求直线ON的解析式.
| 3 |
| 5 |
(1)求这两个函数的解析式;
(2)若N为一次函数y=nx+b图象上的一点,且S△OBN:S△AON=1:2,求直线ON的解析式.
考点:两条直线相交或平行问题
专题:
分析:(1)先根据待定系数法确定正比例函数解析式为y=
x;再利用两点间的距离公式计算出OA=10,则B点坐标为(0,6),然后根据待定系数法确定直线的解析式;
(2)根据S△OBN:S△AON=1:2可知N点的纵坐标是A点的纵坐标的
,所以N点的纵坐标是2,代入一次函数的解析式求得横坐标,而后利用待定系数法求得解析式.
| 3 |
| 4 |
(2)根据S△OBN:S△AON=1:2可知N点的纵坐标是A点的纵坐标的
| 1 |
| 3 |
解答:解:(1)∵A点在正比例函数y=mx上,
∴6=8m,
解得:m=
,
∴正比例函数为;y=
x,
∵A(8,6),
∴OA=10,
∵OB=
OA,
∴OB=6,
∴B(6,0)或(-6,0)
∴
,或
解得:
,或
∴一次函数的解析式为:y=3x-18或y=
x+
,
(2)设N点的坐标为(m,n),
已知S△OBN:S△AON=1:2,
当点N在直线y=3x-18上,AB之间,NB:NA=1:2,得N(
,2),
当点N在直线y=3x-18上,AB延长线上,AB=BN;得N(4,-6),
当点N在直线y=
x+
上,AB之间,NB:NA=1:2,得N(-
,2),
当点N在直线y=
x+
上,AB延长线上,AB=BN;得N(-20,-6),
∴直线ON的解析式为y=
x或y=-
x.
∴6=8m,
解得:m=
| 3 |
| 4 |
∴正比例函数为;y=
| 3 |
| 4 |
∵A(8,6),
∴OA=10,
∵OB=
| 3 |
| 5 |
∴OB=6,
∴B(6,0)或(-6,0)
∴
|
|
解得:
|
|
∴一次函数的解析式为:y=3x-18或y=
| 3 |
| 7 |
| 18 |
| 7 |
(2)设N点的坐标为(m,n),
已知S△OBN:S△AON=1:2,
当点N在直线y=3x-18上,AB之间,NB:NA=1:2,得N(
| 20 |
| 3 |
当点N在直线y=3x-18上,AB延长线上,AB=BN;得N(4,-6),
当点N在直线y=
| 3 |
| 7 |
| 18 |
| 7 |
| 4 |
| 3 |
当点N在直线y=
| 3 |
| 7 |
| 18 |
| 7 |
∴直线ON的解析式为y=
| 3 |
| 10 |
| 3 |
| 2 |
点评:本题考查的是待定系数法求解析式.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
| A、2.5m | B、2.25m |
| C、2m | D、3m |
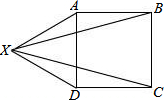 如图,ABCDXA表示一条环形高速公路,X表示一座水库,B,C表示两个大市镇,已知ABCD是一个正方形,XAD是一个等边三角形,假设政府要铺设两条输水管XB和XC,从水库向B,C两个市镇供水,那么着两水管的夹角∠BXC=
如图,ABCDXA表示一条环形高速公路,X表示一座水库,B,C表示两个大市镇,已知ABCD是一个正方形,XAD是一个等边三角形,假设政府要铺设两条输水管XB和XC,从水库向B,C两个市镇供水,那么着两水管的夹角∠BXC=
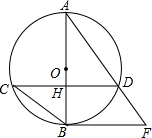 如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.
如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F. 如图,在?ABCD中,O是AC与BD的交点,过点O的直线分别与AB、CD的延长线交于点E、F.当AC与EF满足什么条件时,四边形AECF是菱形?请给出证明.
如图,在?ABCD中,O是AC与BD的交点,过点O的直线分别与AB、CD的延长线交于点E、F.当AC与EF满足什么条件时,四边形AECF是菱形?请给出证明.