题目内容
△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点.
(1)如果沿直线DE折叠成图①的形状,点A落在CE上,当∠A=30°,求∠1的度数.
(2)如果折成图②的形状,当∠A=n°,求∠1+∠2的度数.
(3)如果折成图③的形状,问∠1、∠2、∠A有何关系?

(1)如果沿直线DE折叠成图①的形状,点A落在CE上,当∠A=30°,求∠1的度数.
(2)如果折成图②的形状,当∠A=n°,求∠1+∠2的度数.
(3)如果折成图③的形状,问∠1、∠2、∠A有何关系?

考点:三角形内角和定理,三角形的外角性质,翻折变换(折叠问题)
专题:
分析:(1)翻折问题要在图形是找着相等的量.图1中DE为折痕,有∠A=∠DA′A,再利用外角的性质可得结论∠1=2∠A;
(2)根据图2中∠A与∠DA′E是相等的,再结合四边形的内角和及互补角的性质可得结论∠BDA′+∠CEA′=2∠A;
(3)根据图3中由于折叠∠A与∠DA′E是相等的,再两次运用三角形外角的性质可得结论.
(2)根据图2中∠A与∠DA′E是相等的,再结合四边形的内角和及互补角的性质可得结论∠BDA′+∠CEA′=2∠A;
(3)根据图3中由于折叠∠A与∠DA′E是相等的,再两次运用三角形外角的性质可得结论.
解答:解:(1)如图1,根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,故∠BDA′=2∠A;
∵∠A=30°,
∴∠BDA′=2∠A=60°;
(2)∠1+∠2=2n°,
理由:如图2,在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°,
∴∠A+∠DA′E=360°-∠ADA′-∠A′EA,
∵∠1+∠ADA′=180°,∠2+∠A′EA=180°,
∴∠1+∠2=360°-∠ADA′-∠A′EA,
∴∠1+∠2=∠A+∠DA′E,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠1+∠2=2∠A=2n°;
(3)∠1-∠2=2∠A,
理由:如图3,DA′交AC于点F,
∵∠1=∠A+∠DFA,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2,
∴∠1-∠2=∠A+∠A′,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠1-∠2=2∠A.
∵∠A=30°,
∴∠BDA′=2∠A=60°;
(2)∠1+∠2=2n°,
理由:如图2,在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°,
∴∠A+∠DA′E=360°-∠ADA′-∠A′EA,
∵∠1+∠ADA′=180°,∠2+∠A′EA=180°,
∴∠1+∠2=360°-∠ADA′-∠A′EA,
∴∠1+∠2=∠A+∠DA′E,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠1+∠2=2∠A=2n°;
(3)∠1-∠2=2∠A,
理由:如图3,DA′交AC于点F,
∵∠1=∠A+∠DFA,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2,
∴∠1-∠2=∠A+∠A′,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠1-∠2=2∠A.
点评:此题主要考查了三角形内角和定理以及翻折变换的性质,遇到折叠的问题,一定要找准相等的量,结合题目所给出的条件在图形上找出之间的联系则可.

练习册系列答案
相关题目

 如图,在?ABCD中,O是AC与BD的交点,过点O的直线分别与AB、CD的延长线交于点E、F.当AC与EF满足什么条件时,四边形AECF是菱形?请给出证明.
如图,在?ABCD中,O是AC与BD的交点,过点O的直线分别与AB、CD的延长线交于点E、F.当AC与EF满足什么条件时,四边形AECF是菱形?请给出证明.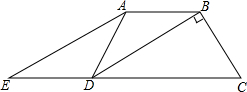 如图,在四边形ABCD中,AB∥DC,DB平分∠ADC,E是CD的延长线上一点,且∠AEC=
如图,在四边形ABCD中,AB∥DC,DB平分∠ADC,E是CD的延长线上一点,且∠AEC= 学校准备在校园里利用围墙的一段,围成一个矩形植物园.如图所示:现已备足可以砌100米长的墙的材料,请设计一种能使围成面积最大的砌墙方法.
学校准备在校园里利用围墙的一段,围成一个矩形植物园.如图所示:现已备足可以砌100米长的墙的材料,请设计一种能使围成面积最大的砌墙方法.