题目内容
7. 把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.(1)连接BE,求证:四边形BFDE是菱形,并说明理由;
(2)若AB=8cm,BC=16cm,求线段DF及折痕EF的长.
分析 (1)由EF垂直并平分BD BD与EF交于点O,四边形ABCD是矩形,易证得△DOE≌△BOF,继而证得DE=BE=BF=DF,则可得四边形BFDE是菱形;
(2)首先设DF=x,则FC=16-x,在Rt△EBF中,利用勾股定理即可求得菱形的边长,再过点E作EG⊥BC于G,即可求得答案.
解答 解:(1)四边形BFDE是菱形.
由折叠可知:EF垂直并平分BD BD与EF交于点O,
则BE=DE BF=DF,
∵四边形ABCD是矩形,
∴DE∥BF,
∴∠EDO=∠FBO,
在△DOE和△BOF中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{OB=OD}\\{∠EOD=∠FOB}\end{array}\right.$,
∴△DOE≌△BOF(ASA),
∴DE=BF, ∴DE=BE=BF=DF,
∴DE=BE=BF=DF,
∴四为形BFDE为菱形;
(2)设DF=x,则FC=16-x,
在Rt△EBF中,由勾股定理得:FC2+DC2=DF2,
即82+(16-x)2=x2,
解得:x=10,
即DF的长为10,
过点E作EG⊥BC于G,则GF=4,
由勾股定理得:EF=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$.
点评 此题考查了矩形的性质、菱形的判定与性质、勾股定理以及折叠的性质.注意掌握折叠前后图形的对应关系,掌握方程思想的应用是解此题的关键.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 方程的解等于零,就是增根 | |
| B. | 使最简公分母的值为零的解是增根 | |
| C. | 使分子的值为零的解是增根 | |
| D. | 只有使所有分母的值为零的解才是增根 |

 如图,三角形ABC在平面直角坐标系中,
如图,三角形ABC在平面直角坐标系中,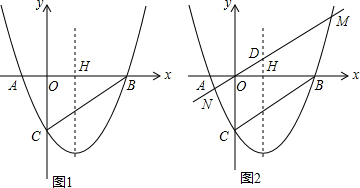
 已知直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).
已知直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).