题目内容
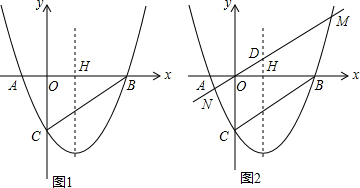
12.如图,已知抛物线y=x2+bx+c交x轴于点A(-1,0)B(2,0),交y轴于点C,抛物线的对称轴交x轴于点H,直线y=kx(k>0)交抛物线于点M,N(点M在N的右侧),交抛物线的对称轴于点D.(1)求b和c的值;
(2)如图(1),若将抛物线y=x2+bx+c沿y轴方向向上平移$\frac{5}{4}$个单位,求证:所得新抛物线图象与直线BC无交点;
(3)如图(2),若MN∥BC.
①连接CD、BM,判断四边形CDMB是否为平行四边形,说明理由;
②以点D为圆心,DH长为半径画圆⊙D,点P为抛物线上一点,Q点在⊙D上,试求线段PQ长的最小值.
分析 (1)把A、B两点的坐标代入物线y=x2+bx+c中,得到一个方程组,求解即可;
(2)根据题意得出新的解析式,再设直线BC为y=kx+b,求出直线BC的解析式,由此联立方程组,得到一个一元二次方程,再求出△的值,即可得出答案;
(3)根据两点间距离公式,利用配方法转化为二次函数最值问题即可解决.
解答 解:(1)由题意得:
$\left\{\begin{array}{l}{1-b+c=0}\\{4+2b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-1}\\{c=-2}\end{array}\right.$,
则b=-1,c=-2.
(2)∵抛物线为y=(x+1)(x-2)=x2-x-2,沿y轴方向向上平移$\frac{5}{4}$个单位,
∴新抛物线为y=x2-x-$\frac{3}{4}$,
设直线BC为y=kx+b,
由题意得$\left\{\begin{array}{l}{b=-2}\\{2k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
所以直线BC为:y=x-2,
由$\left\{\begin{array}{l}{y=x-2}\\{y={x}^{2}-x-\frac{3}{4}}\end{array}\right.$消去y得到x2-2x+$\frac{5}{4}$=0,
∵△=4-5=-1<0,
∴方程组无解,抛物线与直线BC没有交点.
(3)①∵MN∥BC,
∴k=1,OM>OB,
∴MN≠BC,
∴四边形CDMB不是平行四边形.
②设点P(m,m2-m-2),
∵点D坐标为($\frac{1}{2}$,$\frac{1}{2}$),
∴PD2=(m-$\frac{1}{2}$)2+(m2-m-$\frac{5}{2}$)2=(m-$\frac{1}{2}$)2+[(m-$\frac{1}{2}$)2-$\frac{11}{4}$]2=(m-$\frac{1}{2}$)4-$\frac{9}{2}$(m-$\frac{1}{2}$)2+$\frac{121}{16}$=[(m-$\frac{1}{2}$)2-$\frac{9}{4}$]2+$\frac{10}{4}$,
∴PD2的最小值=$\frac{10}{4}$,
∴PD的最小值=$\frac{\sqrt{10}}{2}$,
∵DQ=$\frac{1}{2}$,
∴线段PQ的最小值=$\frac{\sqrt{10}-1}{2}$.
点评 此题考查了二次函数的综合,用到的知识点是待定系数法确定一次函数、二次函数解析式,解题的关键是利用配方法,转化为二次函数的最值问题,有一定的代数化简技巧,属于中考压轴题.

| A. | x2+5x-1=x(x+5)-1 | B. | x2-9=(x+3)(x-3) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | (x+2)(x-2)=x2-4 |
| A. | 3x2•4x2=12x2 | B. | x3•x3=x5 | C. | (x4)2=x7 | D. | 2a•(-2ab2)2=8a3b4 |
 如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5.
如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5. 把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.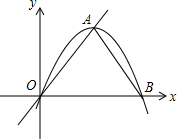 已知抛物线y=ax2+bx(a<0)与x轴的一个交点为B,顶点A在直线y=$\sqrt{3}$x上,O为坐标原点.
已知抛物线y=ax2+bx(a<0)与x轴的一个交点为B,顶点A在直线y=$\sqrt{3}$x上,O为坐标原点. 已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,且AM=BC,点P是AB延长线上的一点,∠PCB=$\frac{1}{2}$∠BAC.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,且AM=BC,点P是AB延长线上的一点,∠PCB=$\frac{1}{2}$∠BAC.