题目内容
16. 已知直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).
已知直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).(1)若点A的坐标为(0,0),点B的坐标为(1,3),则点C的坐标为(0,3).
(2)设抛物线y=ax2+bx的对称轴与x轴交于点D,直线y=ax+b与y轴交于点E,点F的坐标为(1,0),且DE∥CF,点C在直线y=-4x上.
①求抛物线的解析式.
②点P为直线AB上方的抛物线上一点,当S△PAB=$\frac{3}{2}$S△COE时,求点P的坐标.
分析 (1)把A、B两点坐标代入y=ax+b即可解决问题.
(2)①根据两直线平行,k相等列出方程,用方程组解决问题.
②根据S△PAB=$\frac{3}{2}$S△COE,得到S△PAH+S△PHB-S△AHB=$\frac{3}{2}$S△COE,列出方程即可解决问题.
解答 解:(1)把A(0,0),B(1,3)代入y=ax+b得$\left\{\begin{array}{l}{b=0}\\{a+b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=3}\\{b=0}\end{array}\right.$,
∴点C坐标(3,0).
(2)①∵DE∥CF,
∴KDE=KCB,
∵E(0,b),D(-$\frac{b}{2a}$,0),F(1,0),C(a,b),
∴$\frac{a-1}{b}$=$\frac{\frac{b}{2a}}{b}$ ①,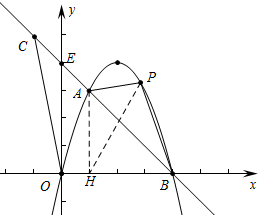
又∵点C在直线y=-4x上,
∴b=-4a ②,
由①②解得a=-1,b=4,
∴抛物线为y=-x2+4x.
②如图,作AH⊥OB于H,连接PH.
由$\left\{\begin{array}{l}{y=-{x}^{2}+4x}\\{y=-x+4}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$,
∴点A(1,3),点B(4,0).点E(0,4),设点P(m,-m2+4m).
由题意S△PAB=$\frac{3}{2}$S△COE,
∴S△PAH+S△PHB-S△AHB=$\frac{3}{2}$S△COE,
∴$\frac{1}{2}$•3•(m-1)+$\frac{1}{2}$•3•(-m2+4m)-$\frac{9}{2}$=$\frac{3}{2}$•$\frac{1}{2}$•4•1,
整理得到m2-5m+5=0,
∴m=$\frac{5±\sqrt{5}}{2}$,
∴点P坐标($\frac{5+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$)或($\frac{5-\sqrt{5}}{2}$,$\frac{5+\sqrt{5}}{2}$).
点评 本题考查抛物线与x轴交点、一次函数、二次函数等知识,解题的关键是把问题转化为解方程组,体现了转化的数学思想,记住两直线平行k相等,题目有点难度,属于中考压轴题.

| A. | $\frac{1}{x}$+$\frac{1}{2x}$=$\frac{1}{3x}$ | B. | $\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{x-y}$ | C. | $\frac{x}{x+1}$+1=$\frac{1}{x+1}$ | D. | $\frac{2}{xy}$-$\frac{1}{y}$=$\frac{2-x}{xy}$ |
 如图,在正方形ABCD外侧,作等边△ADE,AC、BE相交于点F,求∠BFC.
如图,在正方形ABCD外侧,作等边△ADE,AC、BE相交于点F,求∠BFC. 把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.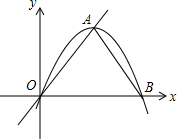 已知抛物线y=ax2+bx(a<0)与x轴的一个交点为B,顶点A在直线y=$\sqrt{3}$x上,O为坐标原点.
已知抛物线y=ax2+bx(a<0)与x轴的一个交点为B,顶点A在直线y=$\sqrt{3}$x上,O为坐标原点. 已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,且AM=BC,点P是AB延长线上的一点,∠PCB=$\frac{1}{2}$∠BAC.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,且AM=BC,点P是AB延长线上的一点,∠PCB=$\frac{1}{2}$∠BAC.
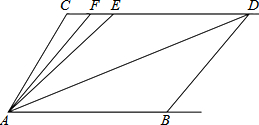 如图,已知CD∥AB,∠C=∠B=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.
如图,已知CD∥AB,∠C=∠B=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.