题目内容
18.在矩形ABCD中,点E在BC上,以AE为边作?AEFG,使点D在AE的对边FG上.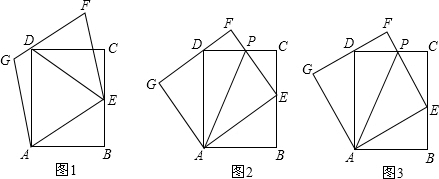
(1)填空:如图1,连接DE,则△ADE的面积=$\frac{1}{2}$四边形AEFG的面积;
并直接写出?AEFG的面积S1与矩形ABCD的面积S2的数量关系;
(2)如图2,EF与CD交于点P,连接PA.
①若∠F=90°,证明:A、E、P、D四点在同一个圆上;并直接说明点D、F、C、E是否在同一个圆上;
(3)如图3,在①的条件下,若AB<BC,AG=AE,且D是FG的中点,EF交CD于点P,试判断以FG为直径的圆与直线PA的位置关系,并说明理由.
分析 (1)作出AE边上的高,分别得出长方形和平行四边形的面积表达式,可得其结果相同,从而说明平行四边形AEFG的面积与矩形ABCD的面积相等.
(2)先求出∠ADC=∠FEA=90°,再根据圆内接四边形的判定定理:“如果一个四边形的一组对角互补,那么这个四边形内接于圆”解答.
(3)过D作DH⊥AP于H,根据∠2+∠3=90°,∠1+∠2=90°,可得∠3=∠1,可求出△ADG∽△AEB;再根据D是FG的中点可求出其相似比为2,再由△ADG与△AEB相似可得其对应边成比例,可求出△ADG∽△AEB∽△APD;最后根据相似三角形的性质可得AD是∠GAH的平分线,可求出DG=DH,故DG=DF,即可解答.
解答 解:(1)如图1,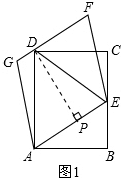
过D点作DP垂直AE于点P;
∵SABCD=AB×AD,
SAEFG=AE×DP=$\frac{AB}{cos∠BAE}$×(AD×cos∠ADP),
∠BAE=∠ADP,
∴SAEFG=AB×AD,
∴SAEFG=SABCD.
∵S△ADE=$\frac{1}{2}$AE×DO,S四边形AEFG=AE×DP,
∴S△ADE=$\frac{1}{2}$S四边形AEFG
(2)如图2,
因为平行四边形AEFG是矩形,四边形ABCD也是矩形;
所以∠ADC=∠FEA=90°,
则∠ADC+∠FEA=180°,
所以A、E、P、D四点在同一个圆上.
(3)相切.
如图3,
过D作DH⊥AP于H;
∵∠2+∠3=90°,∠1+∠2=90°,
∴∠3=∠1,∠2=∠4,
∴△ADG∽△AEB,
∵D是FG的中点,
∴$\frac{AG}{DF}=\frac{GD}{PF}=\frac{AD}{DP}$=2,
在△ADG与△APD中,
∵DF=GD,
∴$\frac{AG}{GD}=\frac{AD}{DP}$=2,
∵∠ADP=∠AGD=90°,
∴△ADG∽△AEB∽△APD,
∴∠1=∠DAP,即AD是∠GAH的平分线,
∴DG=DH=DF,
∵DP=DP,∠DHP=∠DFP=90°,
∴以FG为直径的圆与直线PA相切.
点评 此题是四边形综合题,主要考查了将四边形面积的求法和三角函数相结合.圆内接四边形的判定定理,只要判断出一组对角互补即可.相似三角形的判定定理、角平分形的判定定理及性质,解答此题的关键是作出AE边上的高,作出辅助线.

 作业辅导系列答案
作业辅导系列答案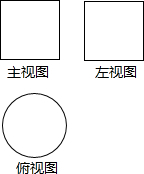 如图所示是一个几何体的三视图,这个几何体的名称是( )
如图所示是一个几何体的三视图,这个几何体的名称是( )| A. | 圆柱 | B. | 三棱锥 | C. | 球 | D. | 圆锥 |
| A. | x2+5x-1=x(x+5)-1 | B. | x2-9=(x+3)(x-3) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | (x+2)(x-2)=x2-4 |
 如图,在正方形ABCD外侧,作等边△ADE,AC、BE相交于点F,求∠BFC.
如图,在正方形ABCD外侧,作等边△ADE,AC、BE相交于点F,求∠BFC. 把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.