题目内容
如图1,△ABC中,M是BC边上中点,E、F分别在AB、AC上,且BE=CF,连接EF,点N是线段EF的中点,连接MN并延长交AB于点P.
(1)求证:∠BAC=2∠BPM;
(2)如图2,当∠A=60°,点F是AC边中点时,探究线段PM与BE的数量关系,并证明你的结论.
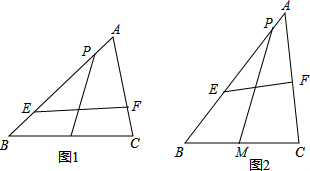
(1)求证:∠BAC=2∠BPM;
(2)如图2,当∠A=60°,点F是AC边中点时,探究线段PM与BE的数量关系,并证明你的结论.
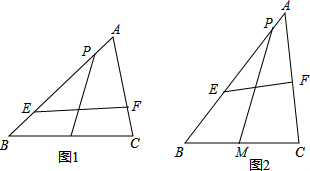
考点:全等三角形的判定与性质,三角形中位线定理
专题:
分析:(1)如图,作辅助线;证明∠KMN=∠KNM(设为α);证明∠QPA=∠BPM=α,∠A=∠Q+∠QPA=2α,即可解决问题.
(2)如图,作辅助线;证明MN=2MK=
λ;证明BE=2λ;证明PM=2MN,即可解决问题.
(2)如图,作辅助线;证明MN=2MK=
| 3 |
解答: 解:(1)如图1,连接BF,取BF的中点K,连接KN、KM;延长MP、CA,交于点Q;
解:(1)如图1,连接BF,取BF的中点K,连接KN、KM;延长MP、CA,交于点Q;
∵M、N分别是BC、EF的中点,
∴MK、NK分别是△BCF、△BEF的中位线,
∴BE=2NK,CF=2MK;而BE=CF,
∴MK=NK,∠KMN=∠KNM(设为α);
∵KM∥AC,KN∥AB,
∴∠Q=∠KMN=α,∠KNM=∠BPM=α;
∴∠QPA=∠BPM=α,∠A=∠Q+∠QPA=2α,
∴∠BAC=2∠BPM.
(2)PM=
BE;
如图2,连接MF、EC,交于点Q;连接QN;
过点Q作QK⊥MN于点K;
由(1)知:∠A=2∠BPM=60°,
∴∠BPM=30°;
∵M、F分别是BC、AC的中点,
∴MF∥AB,EQ=CQ;而EN=FN,
∴ QN∥FC,FC=2QN;
QN∥FC,FC=2QN;
BE∥MQ,BE=2QM;而BE=CF,
∴QM=QN(设为λ),∠QNM=∠QMN=∠BPM=30°;
∵QK⊥MN,且∠QNM=30°,
∴MK=NK=
λ,MN=2MK=
λ;
∵MF∥PB,
∴
=
,而EN=FN,
∴MN=PN,PM=2MN=2
λ;而BE=2MQ=2λ,
∴PM=
BE.
 解:(1)如图1,连接BF,取BF的中点K,连接KN、KM;延长MP、CA,交于点Q;
解:(1)如图1,连接BF,取BF的中点K,连接KN、KM;延长MP、CA,交于点Q;∵M、N分别是BC、EF的中点,
∴MK、NK分别是△BCF、△BEF的中位线,
∴BE=2NK,CF=2MK;而BE=CF,
∴MK=NK,∠KMN=∠KNM(设为α);
∵KM∥AC,KN∥AB,
∴∠Q=∠KMN=α,∠KNM=∠BPM=α;
∴∠QPA=∠BPM=α,∠A=∠Q+∠QPA=2α,
∴∠BAC=2∠BPM.
(2)PM=
| 3 |
如图2,连接MF、EC,交于点Q;连接QN;
过点Q作QK⊥MN于点K;
由(1)知:∠A=2∠BPM=60°,
∴∠BPM=30°;
∵M、F分别是BC、AC的中点,
∴MF∥AB,EQ=CQ;而EN=FN,
∴
 QN∥FC,FC=2QN;
QN∥FC,FC=2QN;BE∥MQ,BE=2QM;而BE=CF,
∴QM=QN(设为λ),∠QNM=∠QMN=∠BPM=30°;
∵QK⊥MN,且∠QNM=30°,
∴MK=NK=
| ||
| 2 |
| 3 |
∵MF∥PB,
∴
| MN |
| PN |
| EN |
| FN |
∴MN=PN,PM=2MN=2
| 3 |
∴PM=
| 3 |
点评:该题主要考查了三角形的中位线定理及其应用问题;解题的关键是作辅助线,构造三角形的中位线;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 已知线段AB,阅读下列语句,分别画出相应的图形.
已知线段AB,阅读下列语句,分别画出相应的图形. 从楼房顶向下看,如图.一个为直角的墙角,直角边4米,一根长为5米的绳,一端拴在直角顶点处,另一端系着一只小羊P,小羊能活动到的最大面积是
从楼房顶向下看,如图.一个为直角的墙角,直角边4米,一根长为5米的绳,一端拴在直角顶点处,另一端系着一只小羊P,小羊能活动到的最大面积是 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为 已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,
已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,