题目内容
18.已知满足不等式3(x-2)+5<4(x-1)+6的最小整数解是方程:2x-ax=3的解,则a的值为$\frac{7}{2}$.分析 首先解不等式求得不等式的解集,然后确定解集中的最小整数值,代入方程求得a的值即可.
解答 解:解不等式3(x-2)+5<4(x-1)+6,
去括号,得:3x-6+5<4x-4+6,
移项,得3x-4x<-4+6+6-5,
合并同类项,得-x<3,
系数化成1得:x>-3.
则最小的整数解是-2.
把x=-2代入2x-ax=3得:-4+2a=3,
解得:a=$\frac{7}{2}$.
故答案是:$\frac{7}{2}$.
点评 本题考查了一元一次不等式的解法以及方程的解的定义,正确解不等式求得x的值是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在一次实验中,小英把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.(以下情况均在弹簧所允许范围内)
(1)在这个变化过程中,自变量是所挂物体的质量,因变量是弹簧的长度;
(2)当所挂物体重量为3千克时,弹簧长度为22cm;不挂重物时,弹簧长度为18cm;
(3)请写出y与x的关系式,若所挂重物为7千克时,弹簧长度是多长?
| 所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | … |
(2)当所挂物体重量为3千克时,弹簧长度为22cm;不挂重物时,弹簧长度为18cm;
(3)请写出y与x的关系式,若所挂重物为7千克时,弹簧长度是多长?
13.若$\sqrt{2m+n}$与$\root{m-n-1}{m+5}$是同类二次根式,则$\sqrt{m+n}$的值为( )
| A. | 1 | B. | 4 | C. | 5 | D. | $\sqrt{5}$ |
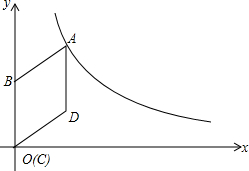 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).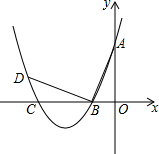 如图,在平面直角坐标系中.顶点为(-4,-1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
如图,在平面直角坐标系中.顶点为(-4,-1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.