Question

7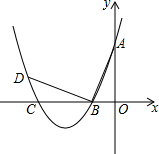．如图，在平面直角坐标系中．顶点为（-4，-1）的抛物线交y轴于点A（0，3），交x轴于B，C两点．
（1）求此抛物线的解析式；
（2）已知点P是抛物线上位于B，C两点之间的一个动点，问：当点P运动到什么位置时，四边形ABPC的面积最大？并求出此时四边形ABPC的面积．
（3）过点B作AB的垂线交抛物线于点D，是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆？若存在，求出圆的半径；若不存在，请说明理由．

Answer 1

分析 （1）利用待定系数法求函数的解析式即可；
（2）由题意可知当P点移动到抛物线的顶点是△PBC的面积最大，根据四边形ABPC的面积的最大值为：S_△ABC+S_△PBC求得即可；
（3）已知∠ABD是直角，若连接圆心和切点（暂定为E），不难看出Rt△OAB、Rt△EBC相似，可据此求出⊙C的半径，再将该半径与点C到对称轴l的距离进行比较即可．

解答 解：（1）根据题意，可设抛物线的解析式为y=a（x+4）²-1，
把点A（0，3）代入得：3=16a-1，
解得a=$\frac{1}{4}$，
所以此抛物线的解析式为y=$\frac{1}{4}$（x+4）²-1；
（2）令y=0，则0=$\frac{1}{4}$（x+4）²-1；
解得x₁=-2，x₂=-6，
∴B（-2，0），C（-6，0），
∴BC=4，
∵S_{四边形ABPC}=S_△ABC+S_△PBC，S_△ABC=$\frac{1}{2}$BC•OA=$\frac{1}{2}$×4×3=6，
∴要使四边形ABPC的面积最大，则△PBC的面积最大，
∴当P点移动到抛物线的顶点时△PBC的面积最大，
∴四边形ABPC的面积的最大值为：S_△ABC+S_△PBC=6+$\frac{1}{2}$×4×1=6+2=8；
（3）如图，设⊙C与BD相切于点E，连接CE，则∠BEC=∠AOB=90°．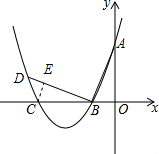
∵A（0，3）、B（-2，0）、C（-6，0），
∴OA=3，OB=2，OC=6，BC=4；
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{13}$，
∵AB⊥BD，
∴∠ABC=∠EBC+90°=∠OAB+90°，
∴∠EBC=∠OAB，
∴△OAB∽△EBC，
∴$\frac{CE}{OB}$=$\frac{BC}{AB}$，即$\frac{CE}{2}$=$\frac{4}{\sqrt{13}}$
∴EC=$\frac{8\sqrt{13}}{13}$．
设抛物线对称轴交x轴于F．
∵抛物线的对称轴x=-4，
∴CF=2≠$\frac{8\sqrt{13}}{13}$，
∴不存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆．

点评 此题是二次函数的综合题，主要考查的是利用待定系数法确定函数解析式、相似三角形的判定和性质、直线与圆的位置关系以及四边形的面积等重要知识点．