题目内容
3.已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=-7-a}\\{x-y=1+3a}\end{array}\right.$的解都是非正数,求a的取值范围.分析 将a看做已知数,求出x与y,根据题意列出不等式组,求出不等式组的解集即可得到a的范围.
解答 解:$\left\{\begin{array}{l}{x+y=-7-a①}\\{x-y=1+3a②}\end{array}\right.$,
①+②得:x=-3+a,
①-②得:y=-4-2a,
所以方程组的解为:$\left\{\begin{array}{l}{x=-3+a}\\{y=-4-2a}\end{array}\right.$,
因为关于x、y的方程组$\left\{\begin{array}{l}{x+y=-7-a}\\{x-y=1+3a}\end{array}\right.$的解都是非正数,所以可得:$\left\{\begin{array}{l}{-3+a≤0}\\{-4-2a≤0}\end{array}\right.$,
解得:-2≤a≤3.
点评 此题考查了二元一次方程组,以及解一元一次不等式组,弄清题意是解本题的关键.

练习册系列答案
相关题目
11.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度:
(1)a=9,b=41,c=40;
(2)a=15,b=16,c=6;
(3)a=2,b=2$\sqrt{3}$,c=4;
(4)a=5k,b=12k,c=13k(k>0)
则构成的是直角三角形的有( )
(1)a=9,b=41,c=40;
(2)a=15,b=16,c=6;
(3)a=2,b=2$\sqrt{3}$,c=4;
(4)a=5k,b=12k,c=13k(k>0)
则构成的是直角三角形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
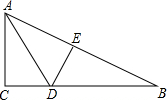 如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )
如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )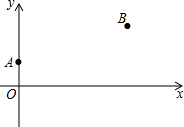 如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.
如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.