题目内容
8.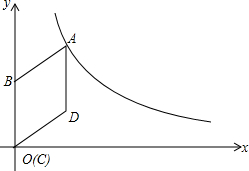 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).(1)求k的值;
(2)若将菱形ABCD向右平移,使菱形的某个顶点落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD平移的距离.
分析 (1)根据点D的坐标为(4,3),即可得出DE的长以及DO的长,即可得出A点坐标,进而求出k的值;
(2)根据D′F′,O′B′的长度即可得出D′、B′的纵坐标,进而利用反比例函数的性质求出OF′BB′的长,即可得出答案;
解答 解:(1)作DE⊥BO,DF⊥x轴于点F,
∵点D的坐标为(4,3),
∴FO=4,DF=3,
∴DO=5,
∴AD=5,
∴A点坐标为:(4,8),
∴xy=4×8=32,
∴k=32;
(2)①∵将菱形ABCD向右平移,使点D落在反比例函数y=$\frac{32}{x}$(x>0)的图象上,
∴DF=3,D′F′=3,
∴D′点的纵坐标为3,
∴3=$\frac{32}{x}$,
x=$\frac{32}{3}$,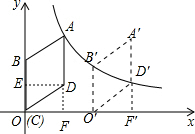
∴OF′=$\frac{32}{3}$,
∴FF′=$\frac{32}{3}$-4=$\frac{20}{3}$,
∴菱形ABCD向右平移$\frac{20}{3}$个单位,点D落在反比例函数y=$\frac{32}{x}$(x>0)的图象上;
②∵将菱形ABCD向右平移,使点B落在反比例函数y=$\frac{32}{x}$(x>0)的图象上,
∴OB=OD=$\sqrt{D{F}^{2}+O{F}^{2}}$=5,
∴B′点的纵坐标为5,
∴5=$\frac{32}{x}$,
∴x=$\frac{32}{5}$,
∴BB′=$\frac{32}{5}$,
∴菱形ABCD向右平移$\frac{32}{5}$个单位,点B落在反比例函数y=$\frac{32}{x}$(x>0)的图象上.
点评 本题主要考查了反比例函数的综合题,利用了菱形的性质,利用了平移的特点,根据已知得出A点坐标是解题关键.

练习册系列答案
相关题目
12.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
| A. | 5 | B. | 6 | C. | 12 | D. | 16 |
20.一电风扇经销商计划花费3100元购进某品牌的A型、B型、C型三种型号电风扇共30台,且每种型号电风扇至少要购进4台,设购进A型电风扇x台,B型电风扇y台,三种型号电风扇进价和售价如下表:
(1)用含x,y的代数式表示购进C型电风扇的台数30-x-y;
(2)求出y与x之间的函数关系式;
(3)求出利润p(元)与x(台)的函数关系式,并求出购进这三种型号电风扇各多少台时所获的利润最大?最大利润是多少?
| 电风扇型号 | A型 | B型 | C型 |
| 进价(元/台) | 90 | 120 | 110 |
| 售价(元/台) | 120 | 160 | 130 |
(2)求出y与x之间的函数关系式;
(3)求出利润p(元)与x(台)的函数关系式,并求出购进这三种型号电风扇各多少台时所获的利润最大?最大利润是多少?
17.数据2、3、2、3、5、3的众数是( )
| A. | 2 | B. | 2.5 | C. | 3 | D. | 5 |

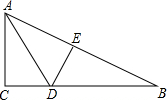 如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )
如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )