题目内容
13.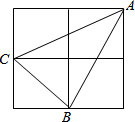 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{5}}{10}$ | C. | $\frac{3\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
分析 首先求出S△ACB的值,再利用勾股定理得出BC的长,再结合三角形面积求出答案.
解答 解:如图所示:S△ACB=4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×1-$\frac{1}{2}$×1×2=$\frac{3}{2}$,
设BC边上的高是h,则$\frac{1}{2}$BC•h=$\frac{3}{2}$,
∵BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴$\frac{1}{2}$×$\sqrt{2}$h=$\frac{3}{2}$,
解得:h=$\frac{3\sqrt{2}}{2}$.
故选:A.
点评 此题主要考查了勾股定理以及三角形面积求法,正确得出△ABC的面积是解题关键.

练习册系列答案
相关题目
1.下列方程中是一元一次方程的是( )
| A. | 5=ab | B. | 2+5=7 | C. | $\frac{x}{2}$+1=x+3 | D. | 3x+5y=8 |
18.敌我相距14千米,得知敌军于1小时前以每小时4千米的速度逃跑,现在我军以每小时7千米的速度追击敌军,在距敌军0.6千米处向敌军开火,48分钟将敌军全部歼灭.问敌军从逃跑到被我军歼灭共花( )小时.
| A. | 5.8 | B. | 6.6 | C. | 6.8 | D. | 7.6 |
5. 如图所示,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前( )米.
如图所示,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前( )米.
 如图所示,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前( )米.
如图所示,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前( )米.| A. | 15 | B. | 20 | C. | 3$\sqrt{7}$ | D. | 24 |
 如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为10.4.
如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为10.4.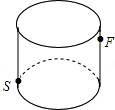 如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm,点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度.
如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm,点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度.