题目内容
2.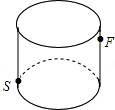 如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm,点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度.
如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm,点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度.
分析 把立体图形展开为平面图形,根据两点之间线段最短,利用勾股定理即可解决问题.
解答 解:如图是圆柱的侧面展开图,线段ST就是蜘蛛走的最短路线,
在Rt△SFN中,∵∠SNF=90°,FN=18-2=16,SN=$\frac{1}{2}$×60=30,
∴SF=$\sqrt{S{N}^{2}+F{N}^{2}}$=$\sqrt{1{6}^{2}+3{0}^{2}}$=34.
∴蚂蚁所走的最短路线的长度为34.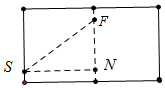
点评 本题考查平面展开图形、两点之间线段最短、勾股定理等知识,解题的关键是把立体图形转化为平面图形解决,属于展开常考题型.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
12.下列是四名同学将命题“不能被2整除的整数是奇数”写出“如果…那么…”的形式,其中正确的是( )
| A. | 如果一个整数能被2整除,那么这个数不是奇数 | |
| B. | 如果一个整数不能被2整除,那么这个数是奇数 | |
| C. | 如果一个整数是奇数,那么这个数不能被2整除 | |
| D. | 如果一个整数不是奇数,那么这个数能被2整除 |
13.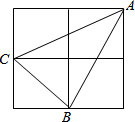 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{5}}{10}$ | C. | $\frac{3\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
10.已知2x•4x=212,则x的值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
17.若代数式$\frac{1}{2}(a-1)$的值不大于-1,则a的取值范围是( )
| A. | a≤2 | B. | a≤-1 | C. | a≤-2 | D. | a≥-3 |
11. 如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.
如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.
 如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.
如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.| A. | 3 | B. | 6 | C. | 8 | D. | $\sqrt{17}$-1 |
 如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )
如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )