题目内容
3.已知,一条抛物线的顶点为E(-1,4),且过点A(-3,0),与y轴交于点C,点D是这条抛物线上一点,它的横坐标为m,且-3<m<-1,过点D作DK⊥x轴,垂足为K,DK分别交线段AE、AC于点G、H.(1)求这条抛物线的解析式;
(2)求证:GH=HK;
(3)当△CGH是等腰三角形时,求m的值.
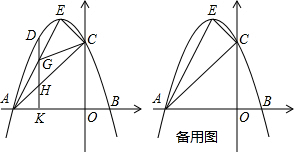
分析 (1)设抛物线的解析式为y=a(x+1)2+4 (a≠0),将点A的坐标代入求得a的值即可求得抛物线的解析式;
(2)先求得直线AE、AC的解析式,由点D的横坐标为m,可求得KG、KH的长(用含m的式子),从而可证明GH=HK;
(3)可分为CG=CH,GH=GC,HG=HC三种情况,接下来依据两点间的距离公式列方程求解即可.
解答 (1)解:∵抛物线的顶点为E(-1,4),
∴设抛物线的解析式为y=a(x+1)2+4 (a≠0).
又∵抛物线过点A(-3,0),
∴4a+4=0,解得:a=-1.
∴这条抛物线的解析式为y=-(x+1)2+4.
(2)设直线AE的解析式为y=kx+b.
∵将A(-3,0),E(-1,4),代入得:$\left\{\begin{array}{l}{-3k+b=0}\\{-k+b=4}\end{array}\right.$,解得:k=2,b=6,
∴直线AE的解析式为y=2x+6.
设直线AC的解析式为y=k1x+b1.
∵将A(-3,0),C(0,3)代入得:$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$,解得:k=1,b=3,
∴直线AC的解析式为y=x+3.
∵D的横坐标为m,DK⊥x轴
∴G(m,2m+6),H(m,m+3).
∵K(m,0)
∴GH=m+3,HK=m+3.
∴GH=HK.
(3)由(2)可知:C(0,3),G(m,2m+6),H(m,m+3)
①若CG=CH,则$\sqrt{{m^2}+{{(2m+3)}^2}}$=$\sqrt{{m^2}+{m^2}}$,整理得:(2m+3)2=m2,解得开平方得:2m+3=±m解得m1=-1,m2=-3,
∵-3<m<-1,
∴m≠-1且m≠-3.
∴这种情况不存在.
②若GC=GH,则$\sqrt{{m^2}+{{(2m+3)}^2}}$=m+3,整理得:2m2+3m=0 解得m1=0(舍去),${m_2}=-\frac{3}{2}$.
③若HC=HG,则$\sqrt{{m^2}+{m^2}}$=m+3,整理得:m2-6m-9=0,解得;m1=3-3$\sqrt{2}$,m2=3+3$\sqrt{2}$(舍去).
综上所述:当△CGH是等腰三角形时,m的值为$-\frac{3}{2}$或$3-3\sqrt{2}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、等腰三角形的判定、两点间的距离公式的应用,依据两点间的距离公式列出关于m的方程是解题的关键.

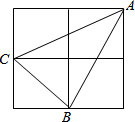 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{5}}{10}$ | C. | $\frac{3\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
 如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.
如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.| A. | 3 | B. | 6 | C. | 8 | D. | $\sqrt{17}$-1 |
| A. |  | B. |  | C. |  | D. |  |
 如图所示,P是等边三角形ABC内一点,且∠APB:∠BPC:∠CPA=3:4:5,求以PA,PB,PC为边的三角形的三个内角的度数.
如图所示,P是等边三角形ABC内一点,且∠APB:∠BPC:∠CPA=3:4:5,求以PA,PB,PC为边的三角形的三个内角的度数. 如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴
如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴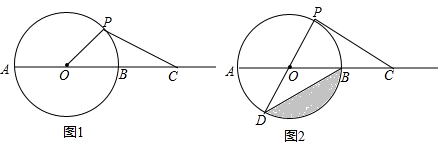
 如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )
如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )