题目内容
1. 如图,某轮船以20海里/小时的速度自西向东航行,在A处测得有一小岛P在北偏东60°的方向上;航行了2小时到达B处,这时测得该小岛P在北偏东30°的方向上,求∠APB的度数及轮船在B处时与小岛P的距离.
如图,某轮船以20海里/小时的速度自西向东航行,在A处测得有一小岛P在北偏东60°的方向上;航行了2小时到达B处,这时测得该小岛P在北偏东30°的方向上,求∠APB的度数及轮船在B处时与小岛P的距离.
分析 (1)首先根据题意可得∠PAB的度数为30°,∠ABP的度数为120°,由三角形的内角和定理可得∠APB的度数;
(2)利用等腰三角形的性质可得PB=AB,易得结果.
解答 解:(1)∵∠DAP=60°,
∴∠PAB=90°-60°=30°,
∵∠PBE=30°,
∴∠ABP=90°+30°=120°,
∴∠APB=180°-∠PAB-∠ABP=180°-30°-120°=30°,
∴∠APB的度数为30°;
(2)∵∠PAB=∠APB=30°,
∴△PAB为等腰三角形,
∴PB=AB=20×2=40(海里)
∴B处时与小岛P的距离为40海里.
点评 本题主要考查了方向角及等腰三角形的性质,证得△PAB为等腰三角形是解答此题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
6.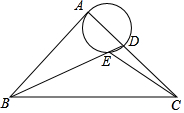 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )| A. | 2$\sqrt{2}$-2 | B. | $\sqrt{5}-2$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}-1$ |
10.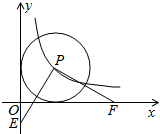 如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
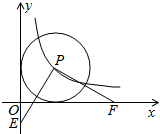 如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )| A. | 6 | B. | 5 | C. | 4 | D. | 2$\sqrt{5}$ |
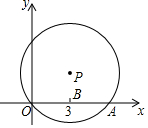 如图所示,在平面直角坐标系中,点P在第一象限,⊙P与x轴交于O、A两点,点B是OA的中点,点B的坐标为(3,0),⊙P的半径为$\sqrt{13}$,则点P的坐标为(3,2).
如图所示,在平面直角坐标系中,点P在第一象限,⊙P与x轴交于O、A两点,点B是OA的中点,点B的坐标为(3,0),⊙P的半径为$\sqrt{13}$,则点P的坐标为(3,2).