题目内容
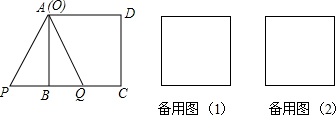
1.如图,△ABC是等腰直角三角形,AB=4,∠ACB=90°,MA⊥AB,动点P、Q分别从A,C同时出发,沿射线AM、AC方向运动,Q的运动速度为1单位/秒,P点运动速度是$\sqrt{2}$单位/秒,设它们运动时间为t(s),线段PB交射线AC于D点,(1)当t=1时,求证:△PBQ是等腰直角三角形.
(2)过D点作DE⊥BD交BQ延长线于E点,问△ABE的面积是否是一个定值?如果是,求出这个定值;如果不是,请说明理由.
(3)直接写出当t=4-2$\sqrt{2}$时,PE∥DQ.
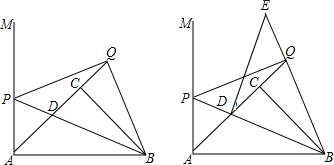
分析 (1)如图1中,作PN⊥AQ垂足为N,只要证明△PQN≌△QBC即可解决问题.
(2)△ABE的面积是定值,如图2中,作DN⊥AB于N,EK⊥ND于K,EG⊥AB于G,连接AE,只要证明△KDE≌△NBD,即可得到EG=KN=AB,由此即可解决问题.
(3)如图3中,连接PE,作PN⊥AC于N,首先证明BQ=BD,再根据PN∥BC得$\frac{BC}{PN}$=$\frac{CD}{DN}$,列出方程即可.
解答 (1)证明:如图1中,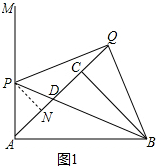 作PN⊥AQ垂足为N.
作PN⊥AQ垂足为N.
∵AC=CB,∠ACB=90°,MA⊥AB
∴∠CAB=∠CBA=∠MAQ=45°,
在RT△PNA中,∵AP=$\sqrt{2}$t,∠PAN=45°,
∴PN=AN=t=CQ,AC=NQ=BC,
在△PQN和△QBC中,
$\left\{\begin{array}{l}{PN=CQ}\\{∠PNQ=∠BCQ}\\{QN=BC}\end{array}\right.$,
∴△PQN≌△QBC,
∴PQ=QB,∠PQN=∠QBC,
∵∠QBC+∠CQB=90°,
∴∠PQN+∠BQC=90°,
∴∠PQB=90°,
∴△PQB是等腰直角三角形.
(2)△ABE的面积是定值,理由如下:
如图2中,作DN⊥AB于N,EK⊥ND于K,EG⊥AB于G,连接AE,
∵∠EDB=90°,△PQB是等腰直角三角形,
∴∠EBD=∠DEB=45°,
∴DE=DB,
∵∠KDE+∠BDN=90°,∠BDN+∠DBN=90°,
∴∠EDK=∠DBN,
在△EDK和△DBH中,
$\left\{\begin{array}{l}{∠K=∠DNB}\\{∠KDE=∠DBN}\\{DE=DB}\end{array}\right.$,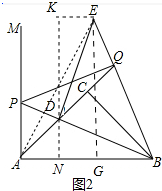
∴△KDE≌△NBD,
∴DK=BN,
∵∠DNA=90°,∠DAN=45°,
∴∠DAN=∠ADN=45°,
∴∠NAD=∠NDA=45°,
∴DN=AN,
∴KN=KD+DN=BN+AN=AB,
∵∠EKN=∠KNG=∠EGN=90°,
∴四边形KNGE是矩形,
∴EG=EN=AB,
∴S△ABE=$\frac{1}{2}$•AB•EG=$\frac{1}{2}$•AB2=8.
(3)如图3中,连接PE,作PN⊥AC于N
∵PE∥AQ,
∴∠PED=∠EDQ,
∵∠DEQ=∠DPQ=45°,
∴P、D、Q、E四点共圆,
∴∠EPQ=∠EDQ,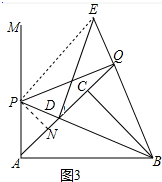
∴∠DEQ=∠QPE,
∴∠BEP=∠BPE,
∵∠BQD=∠BEP,∠BDQ=∠BPE,
∴∠BQD=∠BDQ,
∴BD=BQ,
∵BC⊥AC,
∴CD=CQ=t,
由(1)可知,PN=AN=CQ=t,
∵AB=4,AC=BC=2$\sqrt{2}$,
∴DN=2$\sqrt{2}$-2t,
∵PN∥BC,
∴△DPN∽△DBC,
∴$\frac{BC}{PN}$=$\frac{CD}{DN}$,
∴$\frac{2\sqrt{2}}{t}$=$\frac{t}{2\sqrt{2}-2t}$,
∴t2+4$\sqrt{2}$t-8=0,
∴t=4-2$\sqrt{2}$或-4-2$\sqrt{2}$舍弃.
∴t=(4-2$\sqrt{2}$)秒时,PE∥DQ.
故答案为4-2$\sqrt{2}$.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的性质、四点共圆等知识,解题的关键是添加辅助线构造全等三角形或特殊四边形,学会应用方程的思想解决问题,属于中考压轴题.

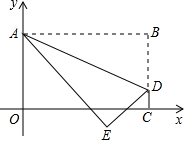 如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )
如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )| A. | $\frac{2}{5}<a<\frac{13}{20}$ | B. | $\frac{2}{5}<a<\frac{11}{20}$ | C. | $\frac{11}{20}<a<\frac{3}{5}$ | D. | $\frac{3}{5}<a<\frac{13}{20}$ |
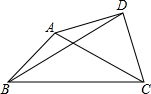 如图四边形ABCD中,AB=4$\sqrt{2}$,BC=12,∠ABC=45°,∠ADC=90°,AD=CD,则BD=2$\sqrt{34}$.
如图四边形ABCD中,AB=4$\sqrt{2}$,BC=12,∠ABC=45°,∠ADC=90°,AD=CD,则BD=2$\sqrt{34}$.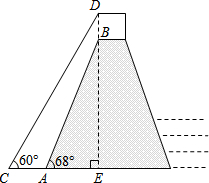 我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.
我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.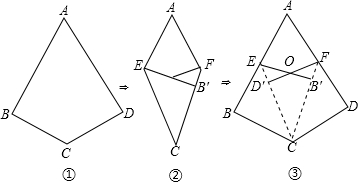
 如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.
如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.