题目内容
6.矩形ABCD中,AB=2$\sqrt{3}$,AD=4,如图,有一个边长为4的等边三角形OPQ,O点与A点重合,PQ在直线BC上,△OPQ沿着BC方向以每秒1个单位长度的速度平移,当O点平移到D点时运动停止,设平移时间为t秒,求两个图形重合部分的面积S关于t的函数关系式,并注明t的取值范围.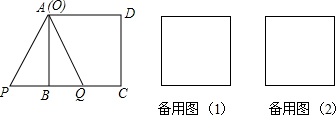
分析 当0≤t≤2时,如图1中作OM⊥BC于M,根据S=S△OPQ-S△PBN即可计算,当2<t≤4时,如图2中,根据S=S△POQ-S△CNQ即可计算.
解答 解:当0≤t≤2时,如图1中,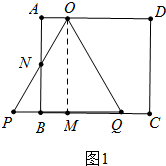 作OM⊥BC于M,
作OM⊥BC于M,
∵四边形ABCD是矩形,
∴∠A=∠ABM=∠OMB=90°,
∴四边形ABMO矩形,
∴AO=BM=t,
在RT△PNB中,∵∠PBN=90°,PB=2-t,∠B=30°,
∴BN=$\sqrt{3}$(2-t),
S=S△OPQ-S△PBN=4$\sqrt{3}$-$\frac{1}{2}$(2-t)($\sqrt{3}$(2-t)=4$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(2-t)2=-$\frac{\sqrt{3}}{2}$t2+2$\sqrt{3}$t+2$\sqrt{3}$,
当2<t≤4时,如图2中,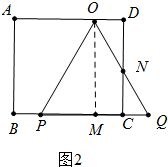
S=S△POQ-S△CNQ=4$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(t-2)2=-$\frac{\sqrt{3}}{2}$t2+2$\sqrt{3}$t+2$\sqrt{3}$,
综上所述s=-$\frac{\sqrt{3}}{2}$t2+2$\sqrt{3}$t+2$\sqrt{3}$,(0≤t≤4).
点评 本题考查动点问题、矩形的性质、三角形的面积等知识,解题的关键是学会分类讨论,正确画出图形,属于中考常考题型.

练习册系列答案
相关题目
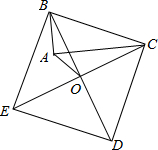 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.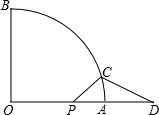 如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.
如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.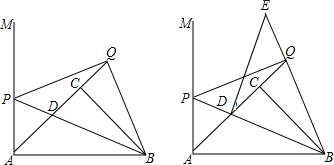
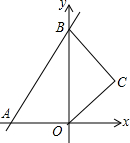 如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为$\sqrt{3}$+1.
如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为$\sqrt{3}$+1.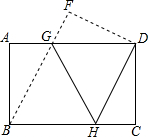 将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.
将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.