题目内容
13. 如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.
如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.
分析 要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果.
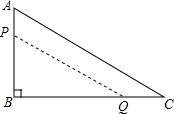
解答  解:如图所示:
解:如图所示:
△BCD是等腰直角三角形,△ACD是等边三角形,
在Rt△BCD中,CD=$\sqrt{B{C}^{2}+B{D}^{2}}$=4$\sqrt{2}$cm,
则BE=$\frac{1}{2}$CD=2$\sqrt{2}$cm,
在Rt△ACE中,AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=2$\sqrt{6}$cm,
答:从顶点A爬行到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.
故答案为:(2$\sqrt{2}$+2$\sqrt{6}$).
点评 此题考查了平面展开-最短路径问题,本题就是把图②的几何体表面展开成平面图形,根据等腰直角三角形的性质和等边三角形的性质解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.方程$\frac{1}{x}-\frac{1-x}{2x}=1$去分母后的结果正确的是( )
| A. | 2-1-x=1 | B. | 2-1+x=1 | C. | 2-1+x=2x | D. | 2-1-x=2x |
 如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.
如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.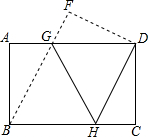 将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.
将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.




