题目内容
12.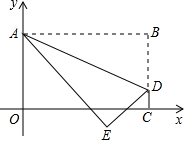 如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )
如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )| A. | $\frac{2}{5}<a<\frac{13}{20}$ | B. | $\frac{2}{5}<a<\frac{11}{20}$ | C. | $\frac{11}{20}<a<\frac{3}{5}$ | D. | $\frac{3}{5}<a<\frac{13}{20}$ |
分析 先判断出△AEM∽EDN得出ME,EN,AB,再过点E作EF⊥AB于F,EF分别与 AD、OC交于点G、H,过点D作DP⊥EF于点P,首先利用勾股定理求得线段DP的长,从而求得线段BF的长,再利用△AFG∽△ABD得到比例线段求得线段FG的长,最后求得a的取值范围.
解答 解:
如图,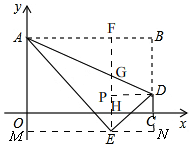
过点E作EM⊥y轴于M,交BC延长线于N,
∵∠AME=∠DNE=90°,∠AEM=∠DEN,
∴△AEM∽EDN,
∴$\frac{AM}{EN}=\frac{EM}{DN}$①,
设AM=BN=m,ME=n,
∴EN=MN-ME=3$\sqrt{5}$-n,DN=BN-BD=m-3
代入①得,$\frac{m}{3\sqrt{5}-n}=\frac{n}{m-3}$②,
根据勾股定理得,m2+n2=(3$\sqrt{5}$)2③,
由②③得n1=3$\sqrt{5}$,m1=0(舍)
n2=2$\sqrt{5}$,m2=5,
∵点A的坐标为(0,4),点D(3$\sqrt{5}$,1),
∴DE=BD=3,
∴AB=3$\sqrt{5}$,AF=2$\sqrt{5}$,E(2$\sqrt{5}$,-1).
过点E作EF⊥AB于F,EF分别与AD、OC交于点G、H,过点D作DP⊥EF于点P,则EP=PH+EH=DC+EH=2,
∵∠AFG=∠ABD=90°,∠FAG=∠BAD,
∴△AFG∽△ABD.
∴$\frac{AF}{AB}=\frac{FG}{BD}$,
即:$\frac{2\sqrt{5}}{3\sqrt{5}}$=$\frac{FG}{3}$,
∴FG=2.
∴EG=EF-FG=3.
∴点G的纵坐标为2.
∵y=ax2-4$\sqrt{5}$ax+10=a(x-2$\sqrt{5}$)2+(10-20a),
∴此抛物线y=ax2-4$\sqrt{5}$ax+10的顶点必在直线x=2$\sqrt{5}$上.
又∵抛物线的顶点落在△ADE的内部,
∴此抛物线的顶点必在EG上.
∴-1<10-20a<2,
∴$\frac{2}{5}<a<\frac{11}{20}$.
故选B.
点评 此题是二次函数的综合题,主要考查对折的性质,解本题的关键是要看出抛物线的对称轴是定值,本题的难点是应从哪里入手.

| A. | $\frac{3}{2}$ | B. | $±2\frac{1}{2}$ | C. | $±\frac{3}{2}$ | D. | 2$\frac{1}{2}$ |
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
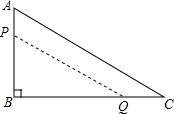 如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.
如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.


