题目内容
14.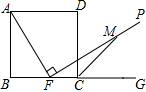 如图,F是正方形ABCD的边BC上的一个点(F与B,C两点不重合),过点F作射线FP⊥AF,∠DCG的平分线交FP于M,求证:AF=FM.
如图,F是正方形ABCD的边BC上的一个点(F与B,C两点不重合),过点F作射线FP⊥AF,∠DCG的平分线交FP于M,求证:AF=FM.
分析 在AB上截取BH=BF,连接HF,则△BHF是等腰直角三角形,AH=FC,证出∠AHF=∠FCM,∠1=∠2,由ASA证明△AHF≌△FCM,得出对应边相等即可.
解答 证明:∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=90°=∠DCG,
∵CM平分∠DCG,
∴∠DCM=$\frac{1}{2}$∠DCG=45°,
∴∠FCM=90°+45°=135°.
在AB上截取BH=BF,连接HF,如图,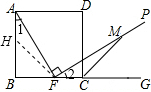 则△BHF是等腰直角三角形,AH=CF,
则△BHF是等腰直角三角形,AH=CF,
∴∠BHF=∠BFH=45°,
∴∠AHF=135°,
∴∠1+∠HFA=45°,∠AHF=∠FCM,
∵FP⊥AF,
∴∠AFM=90°,
∴∠2+∠HFA=45°,
∴∠1=∠2.
在△AHF和△FCM中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AH=FC}\\{∠AHF=∠FCM}\end{array}\right.$,
∴△AHF≌△FCM(ASA),
∴AF=FM.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
 如图所示的表面展开图折叠成正方体后,相对面上的两个数之和均为7,先写出x,y,z的值,再求x+y+z的值.
如图所示的表面展开图折叠成正方体后,相对面上的两个数之和均为7,先写出x,y,z的值,再求x+y+z的值.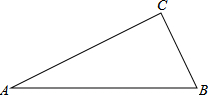 如图,在Rt△ABC中,∠C=90°,
如图,在Rt△ABC中,∠C=90°, 如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.△ABC与△FDE全等吗?说明理由.
如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.△ABC与△FDE全等吗?说明理由. 如图,用代数式表示图中阴影部分的面积,并求当a=4时阴影部分的面积(π取3).
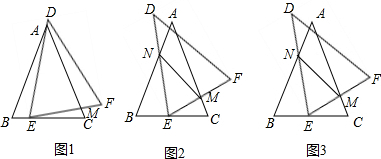
如图,用代数式表示图中阴影部分的面积,并求当a=4时阴影部分的面积(π取3).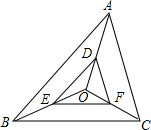 如图,O为△ABC内一点,点D,E,F分别为OA,OB,OC的中点,求证:△DEF∽△ABC.
如图,O为△ABC内一点,点D,E,F分别为OA,OB,OC的中点,求证:△DEF∽△ABC.