题目内容
2.(1)解方程:3x(x-2)=2(2-x)(2)化简:$\frac{3}{{\sqrt{3}}}-{(\sqrt{3}-1)^2}+{(π+\sqrt{3})^0}-\sqrt{27}+|{\sqrt{3}-2}|$.
分析 (1)先移项,再提公因式x-2,转化为两个一元一次方程求解即可;
(2)根据二次根式的化简、零指数幂、绝对值进行计算即可.
解答 解:(1)移项得,3x(x-2)-2(2-x)=0,
提公因式得,(x-2)(3x+2)=0,
x-2=0或3x+2=0,
解得x1=2,x2=-$\frac{2}{3}$;
(2)原式=$\sqrt{3}$-4+2$\sqrt{3}$+1-3$\sqrt{3}$+2-$\sqrt{3}$
=-1-$\sqrt{3}$.
点评 本题考查了二次根式的混合运算以及用因式分解法解一元二次方程,掌握二次根式的化简、零指数幂、绝对值是解题的关键.

练习册系列答案
相关题目
13.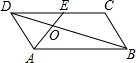 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
10.顺次连接对角线相等的四边形的四边中点所得到的四边形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 平行四边形 |
17. 如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )
如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )
 如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )
如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )| A. | 180° | B. | 240° | C. | 270° | D. | 330° |
 如图,直线y=x-4与x轴、y轴分别交于M、N两点,⊙O的半径为2,将⊙O以每秒1个单位的速度向右作平移运动,当移动时间4-2$\sqrt{2}$或4+2$\sqrt{2}$秒时,直线MN恰好与圆相切.
如图,直线y=x-4与x轴、y轴分别交于M、N两点,⊙O的半径为2,将⊙O以每秒1个单位的速度向右作平移运动,当移动时间4-2$\sqrt{2}$或4+2$\sqrt{2}$秒时,直线MN恰好与圆相切.



 如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.