Question

13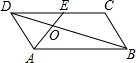．如图，在?ABCD中，E为CD的中点，AE交BD于点O，S_△DCE=12，则S_△AOD等于（　　）

• A． 24
• B． 36
• C． 48
• D． 60

Answer 1

分析 根据相似三角形的性质，先证△DOE∽△BOA，求出相似比为$\frac{1}{2}$，故EO与AO之比为$\frac{1}{2}$，即可求得S_△AOD=2S_△DOE．

解答 解：∵在?ABCD中，E为CD中点，
∴DE∥AB，DE=$\frac{1}{2}$AB，
在△DOE与△BOA中，
∠DOE=∠BOA，∠OBA=∠ODE，
∴△DOE∽△BOA，
∴$\frac{EO}{AO}$=$\frac{DE}{BA}$=$\frac{1}{2}$，
∴S_△AOD=2S_△DOE=2×12=24．
故选（A）．

点评 本题考查了平行四边形的性质以及相似三角形的判定与性质．寻找相似三角形的一般方法是通过平行线构造相似三角形；或依据基本图形对图形进行分解、组合；或作辅助线构造相似三角形．