题目内容
12. 如图,直线y=x-4与x轴、y轴分别交于M、N两点,⊙O的半径为2,将⊙O以每秒1个单位的速度向右作平移运动,当移动时间4-2$\sqrt{2}$或4+2$\sqrt{2}$秒时,直线MN恰好与圆相切.
如图,直线y=x-4与x轴、y轴分别交于M、N两点,⊙O的半径为2,将⊙O以每秒1个单位的速度向右作平移运动,当移动时间4-2$\sqrt{2}$或4+2$\sqrt{2}$秒时,直线MN恰好与圆相切.
分析 作EF平行于MN,且与⊙O切,交x轴于点E,交y轴于点F,设直线EF的解析式为y=x+b,由⊙O与直线EF相切结合三角形的面积即可得出关于b的含绝对值符号的一元一次方程,解方程即可求b值,从而得出点E的坐标,根据运动的相对性,即可得出结论.
解答 解:作EF平行于MN,且与⊙O切,交x轴于点E,交y轴于点F,如图所示.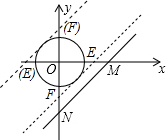
设直线EF的解析式为y=x+b,即x-y+b=0,
∵EF与⊙O相切,且⊙O的半径为2,
∴$\frac{1}{2}$b2=$\frac{1}{2}$×2×$\sqrt{2}$|b|,
解得:b=2$\sqrt{2}$或b=-2$\sqrt{2}$,
∴直线EF的解析式为y=x+2$\sqrt{2}$或y=x-2$\sqrt{2}$,
∴点E的坐标为(2$\sqrt{2}$,0)或(-2$\sqrt{2}$,0).
令y=x-4中y=0,则x=4,
∴点M(4,0).
∵根据运动的相对性,且⊙O以每秒1个单位的速度向右作平移运动,
∴移动的时间为4-2$\sqrt{2}$秒或4+2$\sqrt{2}$秒.
故答案为:4-2$\sqrt{2}$或4+2$\sqrt{2}$.
点评 本题考查了直线与圆的位置关系、一次函数图象上点的坐标特征以及平移的性质,解题的关键是求出点E、M的坐标.本题属于中档题,难度不大,解决该题时,巧妙的利用运动的相对性变移圆为移直线,降低了解题的难度.

练习册系列答案
相关题目
15.下列命题中,假命题是( )
| A. | 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 两直线平行,内错角相等 |
3.用两个全等的等边三角形拼成的四边形是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 等腰梯形 |
 已知直线 l1∥l2,BC=3cm,S△ABC=3cm2,则S△A1BC的高是2cm.
已知直线 l1∥l2,BC=3cm,S△ABC=3cm2,则S△A1BC的高是2cm.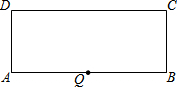 矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP是腰长为5的等腰三角形,则CP的长为2、7或8.
矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP是腰长为5的等腰三角形,则CP的长为2、7或8. (1)先化简,再求值:2x(x-y)-(x-y)2,其中$x=\sqrt{2},y=\sqrt{3}$
(1)先化简,再求值:2x(x-y)-(x-y)2,其中$x=\sqrt{2},y=\sqrt{3}$ 如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为$\frac{11}{5}$.
如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为$\frac{11}{5}$.