Question

10．顺次连接对角线相等的四边形的四边中点所得到的四边形一定是（　　）

• A． 正方形
• B． 矩形
• C． 菱形
• D． 平行四边形

Answer 1

分析 作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=$\frac{1}{2}$AC，GH=$\frac{1}{2}$AC，HE=$\frac{1}{2}$BD，FG=$\frac{1}{2}$BD，再根据四边形的对角线相等可可知AC=BD，从而得到EF=FG=GH=HE，再根据四条边都相等的四边形是菱形即可得解．

解答 解：如图，E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点，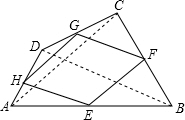
根据三角形的中位线定理，EF=$\frac{1}{2}$AC，GH=$\frac{1}{2}$AC，HE=$\frac{1}{2}$BD，FG=$\frac{1}{2}$BD，
连接AC、BD，
∵四边形ABCD的对角线相等，
∴AC=BD，
所以，EF=FG=GH=HE，
所以，四边形EFGH是菱形．
故选C．

点评 本题考查了菱形的判定和三角形的中位线的应用，熟记性质和判定定理是解此题的关键，注意：有四条边都相等的四边形是菱形．作图要注意形象直观．