题目内容
在半径为4cm 的圆中，挖去一个半径为xcm 的圆面，剩下一个圆环的面积为ycm2，则y与x的函数关系式为( )
A.y=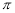
x2-4 B.y=
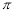(2-x)2 C.y=-(x2+4) D.y=-
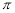x2+16
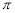
D
【解析】
试题分析：由题意用大圆的面积减去小圆的面积即可得到结果.
由题意得y与x的函数关系式为y=-x2+16，故选D.
练习册系列答案
相关题目
计算：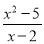 
-
-
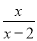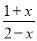
x＋2
【解析】试题分析：根据分式加减的运算法则进行运算即可.
试题解析：原式 在△ABC中，AB=BC，∠ABC=84°，BD是∠ABC的平分线，DE∥BC；求∠EDB的度数.
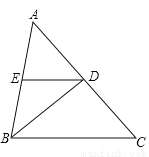
∠EDB=42°.
【解析】试题分析：因为BD是∠ABC的平分线，所以∠ABD=∠CBD，所以∠DBC=84°÷2=42°，因为DE∥BC，所以∠EDB=∠DBC=42°.
试题解析：
∵BD是∠ABC的平分线，
∴∠ABD=∠CBD，
∴∠DBC=84°÷2=42°，
∵DE∥BC，
∴∠EDB=∠DBC=42°. 如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB＝6cm，则△DEB的周长为（ ）
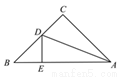
A. 4cm B. 6cm C. 10cm D. 不能确定
B
【解析】∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴DC=DE，
在Rt△AED和Rt△ACD中，
,
∴Rt△AED≌Rt△ACD（HL），
∴AC=AE，
∵AC=BC，
∴∠B=∠CAB=45°，
∴DE=BE，
设DE=BE=x，则DC=x，AE=AC=6－x，
∴BD=x，
∵AC=BC，
∴6－x=... 某广告公司设计一幅周长为12m的矩形广告牌，广告设计费用为1000元/m2.设矩形的一边长为xm，面积为ym2.
(1)求出y与x之间的函数关系式，说明y是不是x的二次函数，并确定x的取值范围；
(2)若x＝3时，广告牌的面积最大，求此时的广告费应为多少？
(1)y＝－x2＋6x，是，0＜x＜6 ；（2）9000元
【解析】试题分析：
（1）矩形的一边长为xm，根据矩形的周长是12m，可得矩形的另一边长为（6－x）m，根据矩形的面积公式即可得出y与x之间的函数表达式；
（2）把x＝3代入函数的解析式得出y的值即为广告牌的最大面积，再乘以1000即为此时的广告费．
试题解析：
【解析】
（1）由题意得出：y ＝x(6－x... （3a-b）（3a+b）-（a+b）2
8a2-2b2-2ab
【解析】试题分析：先根据平方差公式与完全平方公式分别计算，再合并同类项即可.
试题解析：
（3a-b）（3a+b）-（a+b）2=9a2-b2-a2-b2-2ab=8a2-2b2-2ab. （d+f）2等于（ ）
A. d3 -f3 B. d2 +2df+f 2 C. d2 -2f+f 2 D. d2 -df+f 2
B
【解析】根据完全平方公式可得：（d+f）2=d2 +2df+f 2，故选B. （a-b）（a+b）-（a2+b2）
-2b2
【解析】试题分析：先根据平方差公式计算，再合并同类项即可.
试题解析：
（a-b）（a+b）-（a2+b2）=a2-b2-a2-b2=-2b2. 已知图两个中三角形全等，则图2中的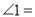
（ ）
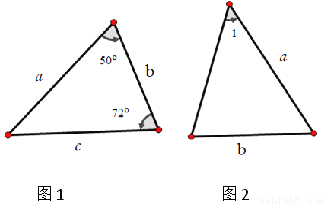
A. 50° B. 58° C. 60° D. 72°
B
【解析】根据三角形的内角和定理求得∠2=180°-50°-72°=58°，根据全等三角形的对应角相等可得∠1=∠2=58°，故选B.