题目内容
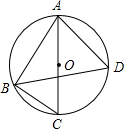 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=60°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=60°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )| A、65° | B、70° |
| C、75° | D、80° |
考点:圆周角定理
专题:
分析:根据圆周角定理以及推论和角平分线的定义可分别求出∠BAC和∠CAD的度数,进而求出∠BAD的度数.
解答:解:∵AC是⊙O的直径,
∴∠ABC=90°,
∵∠C=60°,
∴∠BAC=30°,
∵∠ABC的平分线BD交⊙O于点D,
∴∠ABD=∠DBC=45°,
∴∠CAD=∠DBC=45°,
∴∠BAD=∠BAC+∠CAD=30°+45°=75°,
故选C.
∴∠ABC=90°,
∵∠C=60°,
∴∠BAC=30°,
∵∠ABC的平分线BD交⊙O于点D,
∴∠ABD=∠DBC=45°,
∴∠CAD=∠DBC=45°,
∴∠BAD=∠BAC+∠CAD=30°+45°=75°,
故选C.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,直径所对的圆周角是直角.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
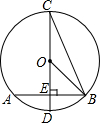 如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、CD,已知⊙O的半径为2,AB=2
如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、CD,已知⊙O的半径为2,AB=2| 3 |
| A、30° | B、45° |
| C、60° | D、15° |
关于x的方程
-
=0的解是x=3,则a的值是( )
| a |
| x+5 |
| 3 |
| x |
| A、6 | B、-6 | C、8 | D、-8 |
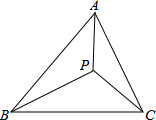 如图,P为△ABC中任意一点.证明:AB+BC+CA>PA+PB+PC.
如图,P为△ABC中任意一点.证明:AB+BC+CA>PA+PB+PC. 如图,l1反映了甲离开A的时间与离A地的距离的关系,l2反映了 乙离开A地的时间与离A地的距离之间的关系,根据图象填空:
如图,l1反映了甲离开A的时间与离A地的距离的关系,l2反映了 乙离开A地的时间与离A地的距离之间的关系,根据图象填空: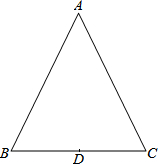 在等腰△ABC中,AB=AC,边BC的中点为D.
在等腰△ABC中,AB=AC,边BC的中点为D.