题目内容
 如图,l1反映了甲离开A的时间与离A地的距离的关系,l2反映了 乙离开A地的时间与离A地的距离之间的关系,根据图象填空:
如图,l1反映了甲离开A的时间与离A地的距离的关系,l2反映了 乙离开A地的时间与离A地的距离之间的关系,根据图象填空:(1)当时间为2小时时,甲离A地
(2)当时间
(3)当时间
考点:一次函数的应用
专题:
分析:(1)设甲离开A的路程s与时间t之间的函数关系式为s甲=kt+b,乙离开A的路程s与时间t之间的函数关系式为s乙=k1t,由函数图象的数据意义求出其解即可;
(2)由函数图象可以直接得出t=4时甲、乙两人离A地距离相等;
(3)由函数图象可以得出t<4时,甲在乙的前面,当时间 t>4时,乙超过了甲.
(2)由函数图象可以直接得出t=4时甲、乙两人离A地距离相等;
(3)由函数图象可以得出t<4时,甲在乙的前面,当时间 t>4时,乙超过了甲.
解答:解:(1)设甲离开A的路程s与时间t之间的函数关系式为s甲=kt+b,乙离开A的路程s与时间t之间的函数关系式为s乙=k1t,由题意,得
,20=4k1,
解得:
,k1=5,
∴s甲=2.5t+10,s乙=5t.
当x=2时,
s甲=15,s乙=10.
故答案为:15,10;
(2)由函数图象,得
当时间t=4时,甲、乙两人离A地距离相等.
故答案为:t=4;
(3)由函数图象可以得出t<4时,甲在乙的前面,当时间t>4时,乙超过了甲.
故答案为:t<4,t>4.
|
解得:
|
∴s甲=2.5t+10,s乙=5t.
当x=2时,
s甲=15,s乙=10.
故答案为:15,10;
(2)由函数图象,得
当时间t=4时,甲、乙两人离A地距离相等.
故答案为:t=4;
(3)由函数图象可以得出t<4时,甲在乙的前面,当时间t>4时,乙超过了甲.
故答案为:t<4,t>4.
点评:本题考查了运用待定系数法求一次函数的解析式的运用,由自变量的值求函数值的运用,解答时分析函数图象的数据的意义是解答本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
下列命题中,错误的是( )
| A、三角形两边之差小于第三边 |
| B、三角形的外角和是360° |
| C、三角形的一边中线能将三角形分成面积相等的两部分 |
| D、正多边形都是中心对称图形 |
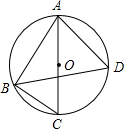 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=60°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=60°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )| A、65° | B、70° |
| C、75° | D、80° |
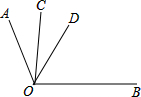 如图,射线OC,OD在∠AOB的内部,OC是∠AOD的平分线,若∠AOB=100°,∠COD=15°,则∠BOD的度数为( )
如图,射线OC,OD在∠AOB的内部,OC是∠AOD的平分线,若∠AOB=100°,∠COD=15°,则∠BOD的度数为( )| A、85° | B、80° |
| C、70° | D、60° |
下列命题的逆命题是真命题的是( )
| A、如果两个角都是直角,那么这两个角相等 |
| B、如果三角形中有一个角是直角,那么另外两个角都是锐角 |
| C、全等三角形的三条边对应相等 |
| D、关于某一条直线对称的两个三角形全等 |
下列事件中,是必然发生的事件是( )
| A、打开电视机,正在播放新闻 |
| B、正数大于负数 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
