题目内容
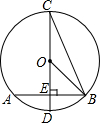 如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、CD,已知⊙O的半径为2,AB=2
如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、CD,已知⊙O的半径为2,AB=2| 3 |
| A、30° | B、45° |
| C、60° | D、15° |
考点:圆周角定理,垂径定理,特殊角的三角函数值
专题:
分析:首先在直角三角形OEB中利用锐角三角函数求得∠EOB的度数,然后利用同弧所对的圆心角和圆周角之间的关系求得∠BCD的度数即可.
解答:解:∵直径CD垂直弦AB于点E,AB=2
,
∴EB=
AB=
,
∵⊙O的半径为2,
∴sin∠EOB=
=
,
∴∠EOB=60°,
∴∠BCD=30°.
故选A.
| 3 |
∴EB=
| 1 |
| 2 |
| 3 |
∵⊙O的半径为2,
∴sin∠EOB=
| EB |
| OB |
| ||
| 2 |
∴∠EOB=60°,
∴∠BCD=30°.
故选A.
点评:本题考查了垂径定理及特殊角的三角函数值,解题的关键是利用垂径定理得到直角三角形.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图,射线AB与AC所组成的角的表示方法不正确的是( )
如图,射线AB与AC所组成的角的表示方法不正确的是( )| A、∠1 | B、∠BAC |
| C、∠CAB | D、∠A |
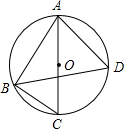 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=60°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=60°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )| A、65° | B、70° |
| C、75° | D、80° |
 如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为( )
如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为( )| A、30° | B、40° |
| C、50° | D、60° |
 已知:A(2,4)、B(2,0),通过原点的直线把△AOB的面积分为1:2的两部分,求这条直线的解析式.
已知:A(2,4)、B(2,0),通过原点的直线把△AOB的面积分为1:2的两部分,求这条直线的解析式.