题目内容
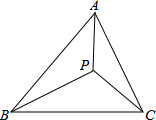如图，P为△ABC中任意一点．证明：AB+BC+CA＞PA+PB+PC．考点：三角形三边关系
专题：证明题
分析：延长BP交AC于D，在△ABD中，AB+AD＞BP+PD，在△DPC中，DP+DC＞PC，求出AB+AC＞BP+PC，同理AC+BC＞AP+BP，AB++BC＞AP+PC，相加即可得出答案．
解答：
证明：延长BP交AC于D，
∵在△ABD中，AB+AD＞BP+PD，
在△DPC中，DP+DC＞PC，
∴AB+AD+DP+DC＞BP+PD+PC，
∴AB+AC＞BP+PC，
同理AC+BC＞AP+BP，AB++BC＞AP+PC，
∴2AB+2AC+2BC＞2AP+2BP+2PC，
即AB+BC+CA＞PA+PB+PC．
证明：延长BP交AC于D，∵在△ABD中，AB+AD＞BP+PD，
在△DPC中，DP+DC＞PC，
∴AB+AD+DP+DC＞BP+PD+PC，
∴AB+AC＞BP+PC，
同理AC+BC＞AP+BP，AB++BC＞AP+PC，
∴2AB+2AC+2BC＞2AP+2BP+2PC，
即AB+BC+CA＞PA+PB+PC．
点评：本题考查了三角形的三边关系定理的应用，主要考查学生运用定理进行推理的能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中，错误的是（ ）
| A、三角形两边之差小于第三边 |
| B、三角形的外角和是360° |
| C、三角形的一边中线能将三角形分成面积相等的两部分 |
| D、正多边形都是中心对称图形 |
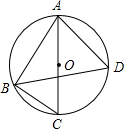如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，∠C=60°，∠ABC的平分线BD交⊙O于点D，则∠BAD的度数是（ ）| A、65° | B、70° |
| C、75° | D、80° |
下列命题的逆命题是真命题的是（ ）
| A、如果两个角都是直角，那么这两个角相等 |
| B、如果三角形中有一个角是直角，那么另外两个角都是锐角 |
| C、全等三角形的三条边对应相等 |
| D、关于某一条直线对称的两个三角形全等 |