题目内容
12.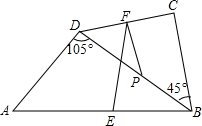 如图,点P是四边形ABCD的对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=45°.∠ADB=105°,试探究EF与PF之间的数量关系,并证明.
如图,点P是四边形ABCD的对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=45°.∠ADB=105°,试探究EF与PF之间的数量关系,并证明.
分析 连接PE,由三角形中位线定理可知PF=PE,且∠EPF=120°,过点P作PG⊥EF,由直角三角形的性质可求得FG=$\frac{\sqrt{3}}{2}$PF,可求得EF=$\sqrt{3}$PF.
解答 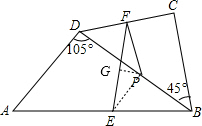 解:EF=$\sqrt{3}$PF.证明如下:
解:EF=$\sqrt{3}$PF.证明如下:
如图,连接PE,
∵P、E分别为BD、AB的中点,
∴PE∥AD,且PE=$\frac{1}{2}$AD,
∴∠ADP+∠EPD=180°,
∴∠EPD=75°,
∵F、P为CD、BD中点,
∴PF∥BC,且PF=$\frac{1}{2}$BC,
∴∠DPF=∠DBC=45°,
∵AD=BC,
∴PF=PE,且∠EPF=75°+45°=120°,
过P作PG⊥EF于点G,则EF=2FG,
在Rt△PFG中,由勾定理可得FG=$\frac{\sqrt{3}}{2}$PF,
∴EF=$\sqrt{3}$PF.
点评 本题主要考查三角形中位线定理,掌握三角形中位线平行且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
3. 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )
已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )
 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )
已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )| A. | 2sin50° | B. | 2sin40° | C. | 2tan50° | D. | 2tan40° |
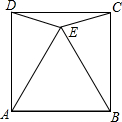 如图所示,点E是正方形ABCD内一点,EA=AB=BE,求∠DEC的度数.
如图所示,点E是正方形ABCD内一点,EA=AB=BE,求∠DEC的度数.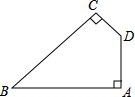 如图,在四边形ABCD中,∠A=∠C=90°,∠B=45°.AB=2$\sqrt{7}$,CD=$\sqrt{5}$,求四边形ABCD的面积.
如图,在四边形ABCD中,∠A=∠C=90°,∠B=45°.AB=2$\sqrt{7}$,CD=$\sqrt{5}$,求四边形ABCD的面积.