题目内容
4.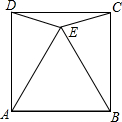 如图所示,点E是正方形ABCD内一点,EA=AB=BE,求∠DEC的度数.
如图所示,点E是正方形ABCD内一点,EA=AB=BE,求∠DEC的度数.
分析 先由正方形和等边三角形的性质得出∠DAE=30°,AD=EA=BC=BE,再由等腰三角形的性质求出∠AED和∠BEC,用周角减去三个角即为所求.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=90°,
∵EA=AB=BE,
∴∠BAE=∠AEB=60°,AD=EA=BC=BE,
∴∠DAE=90°-60°=30°,
∴∠AED=$\frac{1}{2}$(180°-30°)=75°,
同理:∠BEC=75°,
∴∠DEC=360°-75°-75°-60°=150°.
点评 本题考查了正方形的性质、等边三角形的性质、等腰三角形的性质;熟练掌握正方形和等边三角形的性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.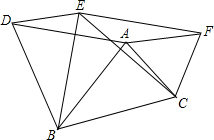 如图,在△ABC中,AB=4,AC=3,BC=5,以三边为边,在BC的同侧分别作三个等边三角形即△ABD,△BCE,△ACF.
如图,在△ABC中,AB=4,AC=3,BC=5,以三边为边,在BC的同侧分别作三个等边三角形即△ABD,△BCE,△ACF.
(1)求证:四边形EFAD是平行四边形;
(2)求四边形EFAD的面积.
 如图,在△ABC中,AB=4,AC=3,BC=5,以三边为边,在BC的同侧分别作三个等边三角形即△ABD,△BCE,△ACF.
如图,在△ABC中,AB=4,AC=3,BC=5,以三边为边,在BC的同侧分别作三个等边三角形即△ABD,△BCE,△ACF.(1)求证:四边形EFAD是平行四边形;
(2)求四边形EFAD的面积.
13.如下表,方程1、方程2、方程3…是按照一定的规律排列的一列方程,解方程3,并将它的解填在表中的空白处.
(1)请写出这列方程中第m个方程,并写出它的解.
(2)用你探究的规律解方程x2-8x-20=0.
| 序号 | 方程 | 方程的解 | |
| 1 | x2+2x-3=0 | x1=1 | x2=-3 |
| 2 | x2+4x-12=0 | x1=2 | x2=-6 |
| 3 | x2+6x-27=0 | x1=3 | x2=-9 |
| … | … | … | … |
(2)用你探究的规律解方程x2-8x-20=0.
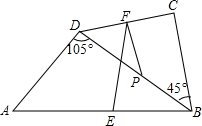 如图,点P是四边形ABCD的对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=45°.∠ADB=105°,试探究EF与PF之间的数量关系,并证明.
如图,点P是四边形ABCD的对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=45°.∠ADB=105°,试探究EF与PF之间的数量关系,并证明.