题目内容
15.解方程:($\frac{{x}^{2}}{x-1}$)2-$\frac{3{x}^{2}}{x-1}$-4=0.分析 用换元法可以解答此方程.
解答 解:设$\frac{{x}^{2}}{x-1}=a$,
a2-3a-4=0,
∴(a-4)(a+1)=0,
解得,a=4或a=-1,
∴$\frac{{x}^{2}}{x-1}=4$或$\frac{{x}^{2}}{x-1}=-1$,
解得,x=2或x=$-\frac{1}{2}±\frac{\sqrt{5}}{2}$,
检验:当x=2或x=$-\frac{1}{2}±\frac{\sqrt{5}}{2}$时,x-1≠0,
故原分式方程的解是x1=2,${x}_{2}=-\frac{1}{2}-\frac{\sqrt{5}}{2}$,${x}_{3}=-\frac{1}{2}+\frac{\sqrt{5}}{2}$.
点评 本题考查解分式方程,解题的关键是会用换元法解方程,注意最后要检验.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕C点顺时针方向旋转90°后,A点的坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕C点顺时针方向旋转90°后,A点的坐标为( )
 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕C点顺时针方向旋转90°后,A点的坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕C点顺时针方向旋转90°后,A点的坐标为( )| A. | ($\sqrt{26}$,0) | B. | (0,7) | C. | ($\sqrt{26}$,1) | D. | (7,0) |
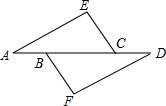 如图,在△AEC和△DBF中,∠E=∠F,点A、B、C、D在同一条直线上,AB=CD、CE∥BF,求证:△AEC≌△DBF.
如图,在△AEC和△DBF中,∠E=∠F,点A、B、C、D在同一条直线上,AB=CD、CE∥BF,求证:△AEC≌△DBF.