题目内容
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)当P也是AD边中点时,求AF的值;
(3)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
(4)当点F与点E重合时,设PF交CD于点G,试判断∠GAE与∠BAE的大小关系并说明理由.

(1)求证:△PFA∽△ABE;
(2)当P也是AD边中点时,求AF的值;
(3)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
(4)当点F与点E重合时,设PF交CD于点G,试判断∠GAE与∠BAE的大小关系并说明理由.

考点:相似三角形的判定与性质
专题:
分析:(1)先证明∠PAF=∠AEB,再由∠PFA=∠ABE=90°,即可证出△PFA∽△ABE.
(2)当P是AD的中点时,AP=2,由△PFA∽△ABE,得出
=
,即
=
,∴AF=
;
(3)分两种情况:当△EFP∽△ABE时,则PE∥AB,得出四边形ABEP为矩形.求出PA=EB=2,即x=2;当△PFE∽△ABE,且∠PEF=∠AEB时,先求出∠PAF=∠AEB,AE=
=
=2
,再得出EF=
AE=
,由
=
,求出PE=5,即x=5;
(4)先证明△ECG∽△ABE,求出CG、EG,再证明△AEG∽△ABE,即可得出∠GAE=∠BAE.
(2)当P是AD的中点时,AP=2,由△PFA∽△ABE,得出
| AF |
| BE |
| AP |
| AE |
| AF |
| 2 |
| 2 | ||
2
|
2
| ||
| 5 |
(3)分两种情况:当△EFP∽△ABE时,则PE∥AB,得出四边形ABEP为矩形.求出PA=EB=2,即x=2;当△PFE∽△ABE,且∠PEF=∠AEB时,先求出∠PAF=∠AEB,AE=
| AB2+BE2 |
| 42+22 |
| 5 |
| 1 |
| 2 |
| 5 |
| PE |
| AE |
| EF |
| EB |
(4)先证明△ECG∽△ABE,求出CG、EG,再证明△AEG∽△ABE,即可得出∠GAE=∠BAE.
解答:(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,AB=BC=AD=4,
∴∠ABE=90°.
∴∠PAF=∠AEB.
又∵PF⊥AE,
∴∠PFA=∠ABE=90°.
∴△PFA∽△ABE.
(2)解:当P是AD的中点时,AP=2,
∵△PFA∽△ABE,
∴
=
,即
=
,
∴AF=
;
(3)解:分两种情况:
①当△EFP∽△ABE,且∠PEF=∠EAB时,
则有PE∥AB
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
②当△PFE∽△ABE,且∠PEF=∠AEB时,
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE=
=
=2
,
∴EF=
AE=
,
∵
=
,即
=
,
∴PE=5,即x=5;
∴满足条件的x的值为2或5;
(4)∠GAE=∠BAE;
解:如图所示:
 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=4,
∴∠BAE+∠AEB=90°,
∵E是BC的中点,
∴BE=CE=2,
∴AE=
=2
,
∵PE⊥AE,
∴∠AEP=90°,∠AEB+∠CEG=90°,
∴∠CEG=∠BAE,
∴△ECG∽△ABE,
∴
=
,即
=
,
∴CG=1,
∴EG=
=
,
∵
=
=
,
=
=
,
∴
=
,
又∵∠AEP=∠B=90°,
∴△AEG∽△ABE,
∴∠GAE=∠BAE.
∴AD∥BC,AB=BC=AD=4,
∴∠ABE=90°.
∴∠PAF=∠AEB.
又∵PF⊥AE,
∴∠PFA=∠ABE=90°.
∴△PFA∽△ABE.
(2)解:当P是AD的中点时,AP=2,
∵△PFA∽△ABE,
∴
| AF |
| BE |
| AP |
| AE |
| AF |
| 2 |
| 2 | ||
2
|
∴AF=
2
| ||
| 5 |
(3)解:分两种情况:
①当△EFP∽△ABE,且∠PEF=∠EAB时,
则有PE∥AB
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
②当△PFE∽△ABE,且∠PEF=∠AEB时,
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE=
| AB2+BE2 |
| 42+22 |
| 5 |
∴EF=
| 1 |
| 2 |
| 5 |
∵
| PE |
| AE |
| EF |
| EB |
| PE | ||
2
|
| ||
| 2 |
∴PE=5,即x=5;
∴满足条件的x的值为2或5;
(4)∠GAE=∠BAE;
解:如图所示:
 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,∴∠B=∠C=90°,AB=BC=4,
∴∠BAE+∠AEB=90°,
∵E是BC的中点,
∴BE=CE=2,
∴AE=
| 42+22 |
| 5 |
∵PE⊥AE,
∴∠AEP=90°,∠AEB+∠CEG=90°,
∴∠CEG=∠BAE,
∴△ECG∽△ABE,
∴
| CG |
| BE |
| CE |
| AB |
| CG |
| 2 |
| 2 |
| 4 |
∴CG=1,
∴EG=
| 12+22 |
| 5 |
∵
| EG |
| AE |
| ||
2
|
| 1 |
| 2 |
| BE |
| AB |
| 2 |
| 4 |
| 1 |
| 2 |
∴
| EG |
| AE |
| BE |
| AB |
又∵∠AEP=∠B=90°,
∴△AEG∽△ABE,
∴∠GAE=∠BAE.
点评:本题考查了正方形的性质和相似三角形的判定与性质;证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
相关题目
 已知a、b、c这三个有理数在数轴上的位置如图所示,化简:|b-c|-|a-b|+|a+c|.
已知a、b、c这三个有理数在数轴上的位置如图所示,化简:|b-c|-|a-b|+|a+c|. 已知:如图,∠ACB=∠DBC,AC=DB. 求证:AB=DC.
已知:如图,∠ACB=∠DBC,AC=DB. 求证:AB=DC. 如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E,BD,CE相交于点F,BE与CD相等吗?请说明理由.
如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E,BD,CE相交于点F,BE与CD相等吗?请说明理由. 已知,在如图四边形ABCD中,AB∥CD,AB=CD,点A,B,C在⊙O上,AD是⊙O切线,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,
已知,在如图四边形ABCD中,AB∥CD,AB=CD,点A,B,C在⊙O上,AD是⊙O切线,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,
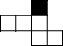
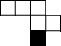
 如图,它需再添一个面,折叠后才能围成一个正方体.图中的黑色小正方形分别由四位同学补画,其中正确的是( )
如图,它需再添一个面,折叠后才能围成一个正方体.图中的黑色小正方形分别由四位同学补画,其中正确的是( )