题目内容
已知a、b、c这三个有理数在数轴上的位置如图所示，化简：|b-c|-|a-b|+|a+c|．考点：整式的加减,数轴,绝对值
专题：计算题
分析：根据题意，由数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，计算即可得到结果．
解答：解：根据数轴上点的位置得：c＜b＜0＜a，且|a|＜|b|＜|c|，
∴b-c＞0，a-b＞0，a+c＜0，
则原式=b-a-a+b-a-c=2b-3a-c．
∴b-c＞0，a-b＞0，a+c＜0，
则原式=b-a-a+b-a-c=2b-3a-c．
点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
如图，等腰梯形ABCD的面积为5已知反比例函数y=
，当1＜x＜2时，y的取值范围是（ ）
| 8 |
| x |
| A、0＜y＜4 | B、1＜y＜2 |
| C、4＜y＜8 | D、y＞8 |
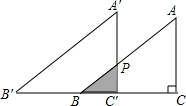如图，△ABC≌A′B′C′，∠C=∠C′=90°，AC=3cm，A′B′=5cm，先将△ABC和△A′B′C′完全重合，再将△ABC固定，△A′B′C′沿CB所在的直线向左以每秒1cm的速度平行移动，设移动x秒后，△ABC与△A′B′C′的重叠部分的面积为ycm2，求：