题目内容
7.某住宅小区的物业管理部门为解决住户停车困难,将一条道路辟为停车场,停车位置如图所示.已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4米,BC=2.2米,∠DCF=40°.请计算停车位所占道路的宽度EF(结果精确到0.1米).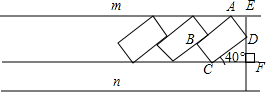
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
分析 在直角三角形中,利用三角函数关系,由已知角度和边求得ED和DF,而求得EF的长.
解答 解:在Rt△CDF中,DC=5.4m,
∴DF=CD•sin40°≈5.4×0.64≈3.46,
在Rt△ADE中,AD=2.2,∠ADE=∠DCF=40°,
∴DE=AD•cos40°≈2.2×0.77≈1.69,
∴EF=DF+DE≈5.15≈5.2(m),
即车位所占街道的宽度为5.2m.
点评 本题考查了解直角三角形的应用,如何从纷杂的实际问题中整理出直角三角形是解决此类题目的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.在菱形ABCD中,∠D:∠A=5:1,若菱形的周长为80cm,则菱形的高DE=( )
| A. | 20cm | B. | 10cm | C. | 10$\sqrt{3}$cm | D. | 20$\sqrt{3}$cm |
 如图,∠1=∠2,∠4=58°,则∠3=58°.
如图,∠1=∠2,∠4=58°,则∠3=58°.