题目内容
17.在Rt△ABC中,∠C=90°,CD为AB边上的中线,若AB=8cm,则CD=4cm.分析 根据直角三角形斜边上的中线等于斜边的一半解答即可.
解答 解:∵∠C=90°,CD为AB边上的中线,
∴CD=$\frac{1}{2}$AB=4cm,
故答案为:4cm.
点评 本题考查的是直角三角形的性质,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为( )
| A. | (-2,-5) | B. | (-2,5) | C. | (2,-5) | D. | (2,5) |
6.下列判断正确的是( )
| A. | 在△ABC 和△DEF中,∠A=40°,∠B=70°;∠D=40°,∠F=80°;则可判定这两个三角形相似 | |
| B. | 有一锐角对应相等的两个直角三角形相似 | |
| C. | 所有的矩形都相似 | |
| D. | 所有的菱形都相似 |
7.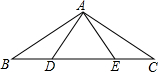 如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )
如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )
 如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )
如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )| A. | ∠B=∠C | B. | AB=AC | C. | ∠ADE=∠AED | D. | ∠B=∠CAE |
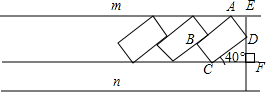
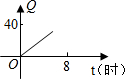

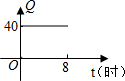
 如图,在△ABC中,D是AB的中点,F是BC边延长线上的点,连结DF交AC于点E.求证:CF:BF=CE:AE.(提示:过点C作CG∥AB)
如图,在△ABC中,D是AB的中点,F是BC边延长线上的点,连结DF交AC于点E.求证:CF:BF=CE:AE.(提示:过点C作CG∥AB)