题目内容
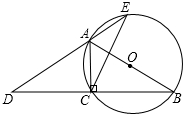 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE.(1)求证:∠B=∠D;
(2)若AB=
| 34 |
考点:圆周角定理,线段垂直平分线的性质,勾股定理
专题:证明题
分析:(1)根据圆周角定理由AB是⊙O的直径得到∠ACB=90°,而DC=CB,根据线段的垂直平分线的判定与性质得AB=AD,于是得到∠B=∠D;
(2)设AC=x,则BC=x+2,在Rt△ABC中,利用勾股定理可计算出解得x=3或-5(舍去),即BC=5,由于∠E=∠B,则∠D=∠E,所以CE=5.
(2)设AC=x,则BC=x+2,在Rt△ABC中,利用勾股定理可计算出解得x=3或-5(舍去),即BC=5,由于∠E=∠B,则∠D=∠E,所以CE=5.
解答:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵DC=CB,
∴AC垂直平分DB,
∴AB=AD,
∴∠B=∠D;
(2)解:设AC=x,则BC=x+2,
在Rt△ABC中,(x+2)2+x2=(
)2,
解得x=3或-5(舍去),即BC=5,
∵∠E=∠B,
∴∠D=∠E,
∴CE=CD=BC=5.
∴∠ACB=90°,
又∵DC=CB,
∴AC垂直平分DB,
∴AB=AD,
∴∠B=∠D;
(2)解:设AC=x,则BC=x+2,
在Rt△ABC中,(x+2)2+x2=(
| 34 |
解得x=3或-5(舍去),即BC=5,
∵∠E=∠B,
∴∠D=∠E,
∴CE=CD=BC=5.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,大圆的直径为8米,小圆的半径为2米,求图中阴影部分的面积.(π≈3.14,结果精确到0.1)
如图,大圆的直径为8米,小圆的半径为2米,求图中阴影部分的面积.(π≈3.14,结果精确到0.1)
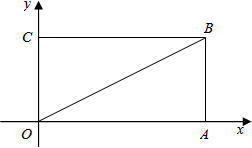 如图,矩形OABC放置在平面直角坐标中,A、C分别在x轴和y轴上,点B在直线y=
如图,矩形OABC放置在平面直角坐标中,A、C分别在x轴和y轴上,点B在直线y=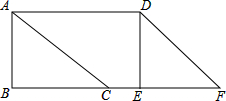 如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A、B、C的对应点分别是D、E、F,连接AD.若有动点P从点D出发,以2cm/s速度沿D→A→C向点C运动,动点Q同时从点B出发,以3cm/s的速度沿B→F→D向点D运动,设P、Q运动时间为t,P、Q两点中一点达到终点,另一点也随之停止运动,请问:
如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A、B、C的对应点分别是D、E、F,连接AD.若有动点P从点D出发,以2cm/s速度沿D→A→C向点C运动,动点Q同时从点B出发,以3cm/s的速度沿B→F→D向点D运动,设P、Q运动时间为t,P、Q两点中一点达到终点,另一点也随之停止运动,请问: