题目内容
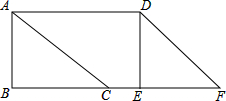 如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A、B、C的对应点分别是D、E、F,连接AD.若有动点P从点D出发,以2cm/s速度沿D→A→C向点C运动,动点Q同时从点B出发,以3cm/s的速度沿B→F→D向点D运动,设P、Q运动时间为t,P、Q两点中一点达到终点,另一点也随之停止运动,请问:
如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A、B、C的对应点分别是D、E、F,连接AD.若有动点P从点D出发,以2cm/s速度沿D→A→C向点C运动,动点Q同时从点B出发,以3cm/s的速度沿B→F→D向点D运动,设P、Q运动时间为t,P、Q两点中一点达到终点,另一点也随之停止运动,请问:(1)当点P在线段DA上运动时,是否存在t的值,使四边形PQCD是等腰梯形?若存在,请求出t的值;若不存在,请说明理由.
(2)在运动过程中,以点P、Q、C、D为顶点的四边形是否能成平行四边形?若可以,请求出相应的t值;若不可以,请说明理由.
考点:等腰梯形的判定,平行四边形的判定
专题:动点型
分析:(1)分为两种情况,当Q在C的左侧时,当Q在C的右侧时,画出图形,根据等腰梯形的性质得出方程,求出即可;
(2)分为三种情况,画出图形,根据平行四边形的性质得出方程,求出即可.
(2)分为三种情况,画出图形,根据平行四边形的性质得出方程,求出即可.
解答: 解:(1)根据题意得:AD=BE=10cm,AB=DE=6cm,BC=EF=8cm,
解:(1)根据题意得:AD=BE=10cm,AB=DE=6cm,BC=EF=8cm,
在Rt△ABC中,由勾股定理得:AC=DF=10,
当P在线段DA上时,0≤t≤5,此时Q在BF上,
当Q在C的左侧时,如图1,过P作PM⊥BF于M,
∵四边形PQCD是等腰梯形,
∴CE=QM=10-8=2,
 则2t=10-(3t-2),
则2t=10-(3t-2),
解得:t=
;此时DP=CQ,
即此时四边形是平行四边形,
故此时不符合题意舍去;
当Q在C的右侧时,如图2,
2t=2(10-3t)+3t-8,
 解得:t=
解得:t=
;
即当点P在线段DA上运动时,存在t的值,使四边形PQCD是等腰梯形,t的值是
;
(2)①当P在AD上,Q在BF上时,即0≤t≤5时,如图3,
当Q在C的左侧时,∵四边形DCQP是平行四边形,AD∥BC,
∴DP=CQ,
 即2t=8-3t,
即2t=8-3t,
解得:t=
;
如图4,当Q在C的右侧时,
∵DP=CQ,
∴2t=3t-8,
t=8,
 ∵0≤t≤5,
∵0≤t≤5,
∴此种情况不符合舍去;
②当P在AC上,Q在BF上时,即5<t≤6时,如图5,
∵AD∥CQ,
∴DP不平行于CQ,此时不符合题意;
③当P在AC上,DF在BF上时,即6<t≤
时,如图6,
 ∵AC∥DF,
∵AC∥DF,
∴CP=DQ,
即10+10-2t=10+10+8-3t,
解得:t=8;
所以在运动过程中,以点P、Q、C、D为顶点的四边形能成平行四边形,相应的t值是
或8.
 解:(1)根据题意得:AD=BE=10cm,AB=DE=6cm,BC=EF=8cm,
解:(1)根据题意得:AD=BE=10cm,AB=DE=6cm,BC=EF=8cm,在Rt△ABC中,由勾股定理得:AC=DF=10,
当P在线段DA上时,0≤t≤5,此时Q在BF上,
当Q在C的左侧时,如图1,过P作PM⊥BF于M,
∵四边形PQCD是等腰梯形,
∴CE=QM=10-8=2,
 则2t=10-(3t-2),
则2t=10-(3t-2),解得:t=
| 8 |
| 5 |
即此时四边形是平行四边形,
故此时不符合题意舍去;
当Q在C的右侧时,如图2,
2t=2(10-3t)+3t-8,
 解得:t=
解得:t=| 12 |
| 5 |
即当点P在线段DA上运动时,存在t的值,使四边形PQCD是等腰梯形,t的值是
| 12 |
| 5 |
(2)①当P在AD上,Q在BF上时,即0≤t≤5时,如图3,
当Q在C的左侧时,∵四边形DCQP是平行四边形,AD∥BC,
∴DP=CQ,
 即2t=8-3t,
即2t=8-3t,解得:t=
| 8 |
| 5 |
如图4,当Q在C的右侧时,
∵DP=CQ,
∴2t=3t-8,
t=8,
 ∵0≤t≤5,
∵0≤t≤5,∴此种情况不符合舍去;
②当P在AC上,Q在BF上时,即5<t≤6时,如图5,
∵AD∥CQ,
∴DP不平行于CQ,此时不符合题意;
③当P在AC上,DF在BF上时,即6<t≤
| 28 |
| 3 |
 ∵AC∥DF,
∵AC∥DF,∴CP=DQ,
即10+10-2t=10+10+8-3t,
解得:t=8;
所以在运动过程中,以点P、Q、C、D为顶点的四边形能成平行四边形,相应的t值是
| 8 |
| 5 |
点评:本题考查了等腰梯形性质,解一元一次方程,平行四边形的性质和判定,平移的性质的应用,注意:用了分类讨论思想,难度偏大.

练习册系列答案
相关题目
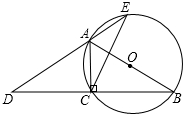 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE.
 如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,
如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0, 如图,用长30cm,宽25cm的长方形地板砖30块摆成一个正方形地面,这块正方形地面的边长是多少?
如图,用长30cm,宽25cm的长方形地板砖30块摆成一个正方形地面,这块正方形地面的边长是多少?